http://surplus.unipa.it/oa/handle/10447/49582
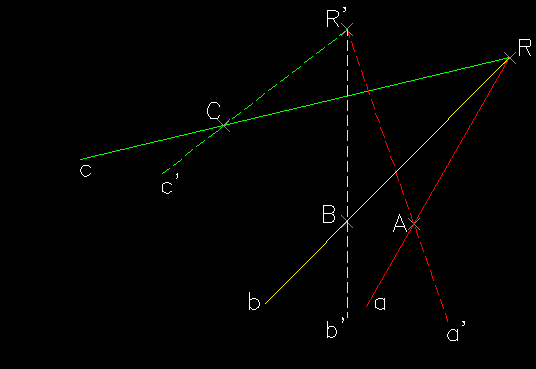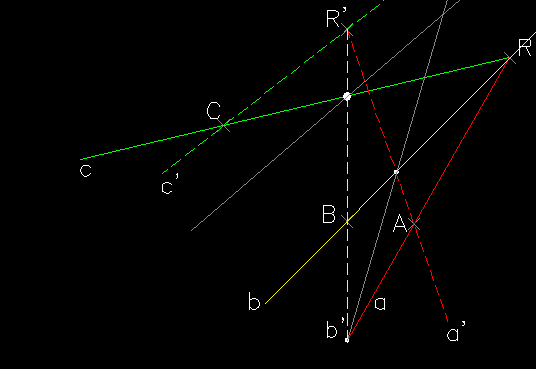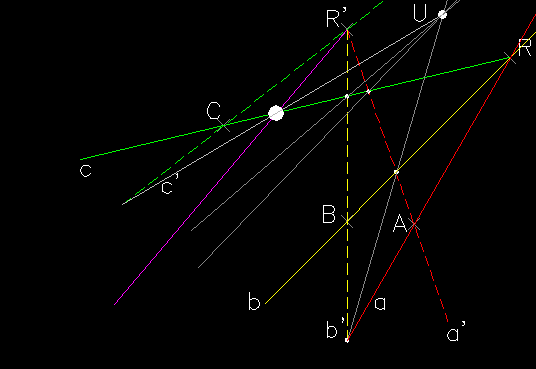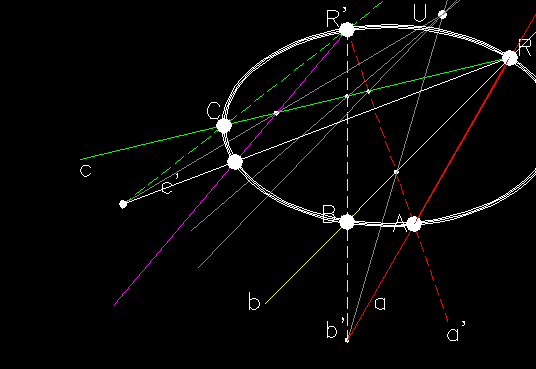
On the other hand, it is not possible to draw conics (ellipse, parabola, hyperbola) in which two conjugate diameters are known, or one diameter and a conjugate chord, or two conjugate chords, or five elements amongst points and tangents; these conditions are very frequent in the applications of the different methods of representation. Our research, starting from the operative limitations highlighted above, intends to translate into programming language AutoLISP, structured with functions of analytical and elementary geometry, the algorithm of descriptive and projective geometry, using procedures and methods proposed by the most illustrious treatisers of the Science of Representation for the construction of conics (A.F. Frézier, M. Chasles, K. Pelz, J.V. Poncelet, J. Steiner). In this paper we report the translation of an algorithm of the construction of an conic from its five known points with projective and homological process .
On the other hand, it is not possible to draw conics (ellipse, parabola, hyperbola) in which two conjugate diameters are known, or one diameter and a conjugate chord, or two conjugate chords, or five elements amongst points and tangents; these conditions are very frequent in the applications of the different methods of representation. Our research, starting from the operative limitations highlighted above, intends to translate into programming language AutoLISP, structured with functions of analytical and elementary geometry, the algorithm of descriptive and projective geometry, using procedures and methods proposed by the most illustrious treatisers of the Science of Representation for the construction of conics (A.F. Frézier, M. Chasles, K. Pelz, J.V. Poncelet, J. Steiner). In this paper we report the translation of an algorithm of the construction of an conic from its five known points with projective and homological process .

ليست هناك تعليقات:
إرسال تعليق