الهندسة الوصفية لطلاب العمارة

الدكتور حسن العيسوي

اعلانات / http://academic.ju.edu.jo/h.isawi/Lists/Announcements/AllItems.aspx
مجموعة الفيسبوك
https://web.facebook.com/groups/331414935481/

==============================================================

الهندسة الوصفية

اذهب إلى التنقلاذهب إلى البحث

الهندسة الوصفية هي علم يبحث طرق تمثيل الأجسام الهندسية المختلفة على سطح مستوي مثل سطح ورقة الرسم (أو على شاشة الحاسوب). وكما يقول غاسبار مونج "الغرض الأساسي للهندسة الوصفية هو الإظهار بدقة أشكال ثلاثية الأبعاد بواسطة رسومات ثنائية الأبعاد الخاضعة لتعريفات صارمة". ،في تعريف مونج يوجد أيضا هدف ثاني وهو "استخلاص من الوصف الدقيق للمجسمات كل ما يليها من شكل ومواضع، وبهذا المعنى، الهندسة الوصفية هي وسيلة بحث للحقيقة العلمية وتعطي أمثلة على الانتقال الدائم من المعروف إلى المجهول".

تعتبر فرع من فروع الهندسة البديهية، أي تبحث من خلال طرق الإسقاط المختلفة (مركزية،موازية)، بيان العلاقة الهندسية بين كل من النقاط والخطوط والمستويات والأجسام في الفراغ، بهدف الوصول، من خلال البحث العلمي المستمر، إلى نتائج وإجراءات هندسية تمكن، المهندس:

• من تنمية قدراته التصورية للفراغ المعماري؛
• من وصف ذلك الفراغ بشكل دقيق من خلال [[ رسومات ثنائية الأبعاد أو نماذج (geometry modeling) ثلاثية الأبعاد.
• من حل مشاكل القياس الخطية والزاوية
• من حل المشاكل المظهرية (Appearance) والتصورية (perception) للأشكال الهندسية.

ويعتمد علم الهندسة الوصفية، كنقطة انطلاق، على مبادئ الهندسة الإسقاطية بكافة نظرياتها وقواعدها المعروفة.

محتويات

• 1مقدمة
• 2تاريخ
• 3تخصصات الرسم
• 4أساليب الهندسة الوصفية
  • 4.1مفاهيم
  • 4.2تأملات
  • 4.3مصادر

مقدمة

علم الهندسة هو أحد فروع الرياضيات الذي يعتنى بدراسة الخواص المترية للخطوط والسطوح من أطوال وزوايا ومساحات وحجوم وكذلك الخواص غير المترية أو الخواص الإسقاطية وهي الخواص التي لا تعتمد على ألاطوال والزوايا ولا تتغير بالإسقاط مثل درجة المنحنى والنسبة المضاعفة وغيرهما وتتشعب تصنيفات الجيومترى إلى عدة شعب فمن حيث أسلوب التمثيل تنقسم إلى الهندسة البيانية
 التي تضم الهندسة الوصفية وغيرها والهندسة التحليلية التي تضم الهندسة التفاضلية والهندسة الحسابية وغيرها ومن حيث
 موضوع التمثيل إلى الهندسة المستوية والهندسة الفراغية كما تنتمى الهندسة الاسقاطية وعلم الطوبولوجى إلى الجيومترى.

في كل من الهندسة الفراغية والتحليلية والتفاضلية و الحسابية يتم التعبير عن الخطوط والسطوح وما يتعلق بهما من مسائل بعلاقات ومعادلات رياضية. أما في الهندسة الوصفية فيتم تمثيل هذه الخطوط والسطوح بالطرق البيانية حيث تكون وسيلة التمثيل في هذه الحالة هي طرق الإسقاط المختلفة، لذا فإن طريقة التمثيل في الهندسة الوصفية تكون برسم مساقط للخطوط والسطوح على اسطح إسقاط أو أسطوانية أو كروية وتبعا لطريقة الإسقاط ونوع سطح الإسقاط فان هذه المساقط تعبر تعبيرا كاملا عن طريق هذه المساقط وكذلك تعيين أبعادها في الفراغ كما أن كثير من المسائل الرياضية المتعلقة بهذه الخطوط والسطوح يكون حلها أحيانا أيسر وأسرع إذا استخدمت الهندسة الوصفية بدلا من الرياضيات التقليدية وبجانب هذا فان الهندسة الوصفية تساعد على تنميه ملكه التصور والتخيل والتفكير الرياضي المنطقي ولها استخدامات عمليه كثيره فنجد أنها تستخدم في رسم الصور المنظورة والظلال التي تضيف على الرسومات المعمارية طابعا يجعلها اقرب إلى الطبيعة كما تستخدم في حل بعض مسائل الفلك والميكانيكا وينتفع بنظرياتها في الفوتوجرامترى
 وعمل الخرائط الجغرافيا والطبوغرافيا اللازمة للمهندس ألمدني في تخطيط مشاريعه من ترع ومصارف وجسور الخ كما تستخدم أيضا في تصميم الآليات الفراغية الميكانيكية وتعيين سرعتها وعجلاتها وتستخدم في الهندسة البحرية وهندسه الطيران في تصميم هياكل السفن والطائرات وتحديد ما يعرف بخطوط المياه وخطوط القطاعات الطولية لجانب السفينة أو الطائرة.

و مع ازدياد استخدام الحاسب الآلي في التصميم الهندسي ازدادت أهمية الهندسة الوصفية وأصبح يعقد لها مؤتمرات عالميه للوقوف
 على طرق استخدامها على الحاسب الآلى في شتى فروع الهندسة فنجد أنها تستخدم بجانب الهندسة الحسابية في تصميم وتطوير
 البرامج المعروفة باسم كاد كما تستخدم في تصميم برامج الحاسب الآلي التي تحلل حركه نقطه في الفراغ وسط مجموعه من العوائق حيث يدخل هذا التحليل في تصميم الإنسان الألى المستخدم حاليا في معظم مصانع السيارات.

و يرجع الفضل في وضع أساس ونظريات علم الهندسة الوصفية إلى العالم الرياضي الفرنسي غاسبار مونج (1764 - 1818) الذي جمع الأسس والنظريات في كتابه المشهور الذي نشر سنه 1779 وهو بعنوان Essais sur les Geometrie Descriptine (اختبارات على الهندسة الوصفية)

تاريخ

منذ الحضارات القديمة في مصر، قد تجلى من الرسومات الهليلجيه في القبور، الاستخدام الصحيح للإسقاطات المتعامدة. 
في القرن الأول قبل الميلاد والقرن الأول بعد الميلاد فيتروفيو Vitruvius، في كتبة ،بعنوان دي اركيتيتورا "De architectura" ،استخدمت المساقط الرأسية والعمودية في رسوم المباني والمصانع ولقبت إكونوكرافيا وأورتوكرافيا (iconography and orthography). في وقت لاحق ياكوبو باروتسو (Jacopo Barozzi) في عملة:"الخمس عناصر للهندسة المعمارية" (five orders of architecture) أستعملت المساقط العمودية التي تشبه طريقة غاسبر مونج (Gaspard monge).
خلال الفترة نفسها، البرتو دورير (1471-1528- Alberto Dürer) عمل رسوم واجراءات تتعلق بالقطع المخروطية، كقطاعات مستوية للمخروط وعمق أيضا دراسة المنظور (perspective).

في 1600 العلماء غوارينو غواريني (Guarino Guarini) وجيرارد ديساركس (Girard Desargues) قد وضعوا
أسس الهندسة الوصفية" كما سميت من قبل الباحث الفرنسي غاسبار مونج (Gaspard Monge 1746- 1818).
في 1700 نشر كتاب "الهندسة الوصفية" التي تطرح فيها القواعد الأساسية لهذا العلم الجديد. القواعد التي تهدف، قبل كل شيء،
ان تمثل على نفس المستوي الاشياء ثلاثية الابعاد. في الوقت الحاضر الهندسة الوصفية تشمل الهندسة الاسقاطية (GEOMETRY PROJECTIVE).التي أهم نتائجها دُرست من قبل العالم جان فيكتور بونسيليت (Jean Victor Poncelet 1788-1867)
تلميذ غاسبار مونج. الهندسة السقاطية عرضت مفهوم هندسي جديد تتعلق باالهيئة الانهائية (النقطة الانهائية، الخط الانهائي والمستوى الانهائي). هذا يؤدي إلى وجود اختلاف كبير مع القاعدة الخامسة لهندسة إقليدس (325 ق.م - 265 ق.م)، في حين ان النسبة
المتبقية من قواعد ارشميدس تبقى صحيحة.

تخصصات الرسم

الرسم هو الوسيلة التي يستخدمها المهندس لتكوين وتواصل المشروع المعماري. ليس الرسم الناتج من بديهية وخبرة فنان ماهر، لأن المهندس المعماري لا يهتم فقط بجماليات المبنى، بل أيضاً بالتحقق من الشكل والمقاس والمواصفات التقنية، وبصفات أخرى كثيرة. والتي يمكن تلخيصها بالمصطلح التحكم المتري والإدراكي. على وجه الخصوص، من خلال استخدام الهندسة الوصفية، يمارس المهندس كيفية إنشاء النماذج الرسومية للأشكال في الفراغ ثلاثي الأبعاد ويدرس خصائصها الهندسية. لتنفيذ رسومات المشروع، يحتاج المهندس أولا إلى مهارته في الرسم الحر، ولكن يجب أيضا ترجمة بديهية وتلقائية الرسم الحر إلى مخططات دقيقة، والتي يمكن رسمها بالمسطرة والفرجار وغيرها من أدوات الرسم التقني. من بين هذه الأدوات منذ أواخر الثمانينات تم ادخال الكمبيوتر، والذي يستخدم الآن على نطاق واسع ويسمح ليس فقط بالرسم ثنائي الأبعاد، بل أيضا بنمذجة مجسمات افتراضية ثلاثية الأبعاد. بدون هذه الأداة، لم يكن من الممكن انجاز الكثير من المشاريع المعمارية الجريئة في السنوات الأخيرة. ونستنتج من ذلك أن تدريس الرسم في كلية الهندسة المعمارية، يجب أن يدمج المقررات التالية:

• الرسم الحر، الذي لا يزال الوسيلة الأكثر فعالية والاسرع لتسجيل فكرة فراغية ما
• الهندسة الوصفية والتي تدرب على ادراك الفراغ وفهم قواعدة وأساليب اظهارة،
• وأخيرا الرسم التقني، بما في ذلك الرسم الرقمي.

هذه التخصصات تساهم جميعها في تشكيل فكر طالب العمارة في السنوات الدراسية الأولى، وإعطائه القدرة على تصميم الفراغات المعمارية المثيرة للاهتمام في السنوات اللاحقة.

أساليب الهندسة الوصفية

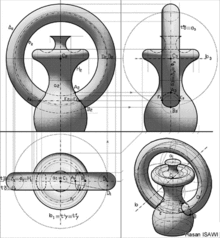
أساليب الهندسة الوصفية (من منظور ،الاسقاط المزدوج العمودي (Monge method) والاسقاط الاكسونومتري (axonometry) تقوم أساسا على عمليتين أساسيتين :الاسقاط والتقاطع.

أساليب الهندسة الوصفية تصنف، بصفة عامة، وفقا لطبيعة مركز الإسقاط م. عندما م تكون نقطة نهائية (على مسافة محدودة)، ألإسقاط يُسمى، إسقاط مركزي (أو منظور) ويُسمى إسقاط متوازي، عندما م تكون نقطة لانهائية (على مسافة لانهائية).

• إسقاط مركزي (أو طريقة المنظور).
  • استرداد منظوري (بالإيطالية: restituzione prospettica ).
  • نظرية الظل من مصدر ضوء على مسافة محدودة.

• إسقاط متوازي
  • إسقاط عمودي
    • إسقاط اكسونومتري
    • طريقة مونج (أو الاسقاط المزدوج العمودي)
    • il metodo delle proiezioni quotate

• • إسقاط مائل
    • إسقاط اكسونومتري
      • • نظرية الظل من مصدر ضوء على مسافة غير محدودة.

مفاهيم

بعض المفاهيم الأساسية للهندسة الوصفية هي :

• تعريف الكيانات الهندسية الاساسية (نقطة، خط، مستوى، اتجاه (نقطة لانهائية) وميلان (خط لانهائي))
• شروط الانتماء : نقطة على خط، خط على سطح ونقطة على سطح.
• حالات التقاطع: بين خطين، بين خط وسطح، وبين سطحيين.
  • شروط التوازي والتعامد (كحالات خاصة للتقاطع).
• شروط التماس وخصوصاً بين المخروطيات وبين الأسطح الدورانية
• التقابل، التماثل، التماثل المعاكس، التألف المنظوري ،التألف، التحول، التحول المعاكس والالتفاف.

تأملات

• في بعض الحالات من المهم الأخذ في الاعتبار النمذجة الرقمية كأداة أساسية لفهم بعض الهندسيات الفراغية التي قد تكون في بعض الأحيان معقدة لدرجة أنها تجعل من المستحيل التحكم بها من خلال الطرق التقليدية، التي تعتمد على الإسقاطات المستوية التي كانت تدرسها تطبيقات الهندسة الوصفية.^[1]
• لا يمكننا تقييم كفاءة تدريس الهندسة الوصفية باستخدام الوسائل التقليدية أو الرقمية أن لم يتم متابعة الطلاب لمدة قد تدوم عدة سنوات أو على الأقل حتى مرحلة مقررات التصميم المتقدمة. وفقط عندئذ يمكن أن نعرف أفضلية هذه أو تلك الطريقة في تدريس الهندسة الوصفية وكفائتها الفعلية في ممارسة تفكير الطلاب على ادراك مفهوم الفراغ وتحقيقه بعد ذلك في تمثيل حجوم معمارية مثيرة للاهتمام من الناحية الهندسية والوظيفية.^[2]

مصادر

1. ^ esperienze di progettazione architettonica assistita Di Massimo Gasperini. Firenze University Press 2006
   esperienze di progettazione architettonica assistita Di Massimo Gasperini. Firenze University Press 2006
2. ^ الوضع الحالي يرغمنا على مناقشة طريقة جديدة لتدريس الهندسة الوصفية / Isawi's blog. 2011 نسخة محفوظة 25 يوليو 2017 على موقع واي باك مشين.
   الوضع الحالي يرغمنا على مناقشة طريقة جديدة لتدريس الهندسة الوصفية / Isawi's blog. 2011 

في كومنز صور وملفات عن: هندسة وصفية

تصنيف:

• هندسة وصفية

restituzione prospettica e inserimento ambientale

Restituzione prospettica e inserimento ambientale

capita spesso a chi lavora nel campo dell'architettura di voler vedere il proprio progetto inserito nel suo contesto reale, e tale fine il metodo della restituzione prospettica permette di determinare le informazioni geometriche di tale contesto.

e per inciso si fotografa il contesto dalla posizione desiderata e poi si va ad inserire la fotografia in un programma vittoriale come AutoCAD per determinare gli elementi fondamentali dell prospettiva che sono il centro di proiezione che coincide con il centro dell’obiettivo della macchina fotografica. e la giacitura del quadro che in questo caso e' parallela al piano sensibile alla luce () della macchine fotografica. e la distanza tra il punto di vista e il quadro che si assume pari alla distanza focale, ovvero quella intercorre tra la pellicola ( o il piano del sensore) e l’obiettivo.

la determinazione del punto di vista

per determinare il punto di vista O, occorre prima determinare la sua proiezione ortogonale  sul piano di quadro pigreco (tale proiezione e' nominata il punto principale O0) .  A secondo l’altezza dell’oggetto rappresentato e quindi l'inclinazione della macchina fotografica, la giacitura del quadro può essere verticale, orizzontale o inclinata.

Nel caso in cui la giacitura del quadro e' verticale, la prospettiva può essere rispettivamente ad una sola fuga, detta prospettiva frontale, o a due fughe detta prospettiva d'angolo.
In generale  occorre determinare le fughe di quattro rette ortogonali  due a due tra loro per determinare la posizione del punto di vista.

poiché la linea dell'orizzonte e' l'immagine della giacitura dei piani orizzontali e quindi rappresenta il luogo dei punti di fuga di tutte le rette orizzontale, e dato che le immagini delle rette parallele tra loro nella realtà sono rette che si incontrano in un stesso punto di fuga. allora occorre congiungere i punti di fuga  di due rette orizzontali Fa, Fb per determinare la linea dell'orizzonte. 

La determinazione di ciascuno di tali punti di fuga avviene prolungando le immagine prospettiche di due  o più segmenti che sono presenti nella fotografia (ad esempio cornici marcapiano, ricorsi della pavimentazione) e che si presuppone che tali segmenti  appartengono nella realta a rette orizzontali parallele tra loro.

Una volta determinate i punti di fuga Fa , Fb di due rette presenti nella fotografia, si va a tracciare la circonferenza Fi1 che ha per diametro tali fughe e che dovrebbe passare per il punto di vista O. questa affermazione e' giustificata dal fatto che la fuga Fa di una reta a rappresenta teoricamente l'immagine del punto improprio della retta a, ovvero l'immagine della direzione di a. tecnicamente, l'immagine della direzione di una retta a si ha come punto d'intersezione del piano di quadro con la retta parallela ad a e passante per il punto di vista O. quindi nel caso in cui ci siano due rette a, b, ortogonali tra loro, si ha che anche le rette passanti per O e parallele a tale rette sono ortogonali tra loro.
e poiche preso qualsiasi punto O* sul perimentro della circonferenza Fi 1 ed unito con i punti Fa e Fb diametrli di fi1, si ha, secondo il teorema di talete un angolo retto in tale punto O*.

Geometric loci

Hasan Isawi

https://www.researchgate.net/project/Geometric-Loci

=====================================================================

يهدف هذا البحث إلى دراسة المحل الهندسي لمراكز الكرات المتماسة لثلاث أسطح رباعية معلومة (الإهليلج، الزائد، المكافئ، الأسطوانة، المخروط). وسيتم التركيز بشكل خاص على تحديد الشروط الكافية والضرورية لوجود مثل هذه الكرات. ومن ثم، استغلال هذه النتائج لنمذجة أسطح عضوية معقدة، وذلك من خلال تحديد السطح المغلف لهذه الكرات.

سيتم استخدام أدوات الهندسة الوصفية والإسقاطية، بالإضافة إلى برمجيات الحاسوب المتخصصة، لتحقيق الأهداف المذكورة.

الهدف النهائي من هذا البحث المساهمة في تطوير أدوات هندسية بديلة لتصميم الأسطح العضوية المعقدة، وتوفير أساس نظري قوي لتعليم طلاب العمارة والتصميم.

la ricerca riguarda la stesura di procedimenti geometrici descrittivi 3d atti alla determinazione dei luoghi geometrici dei punti equidistanti da due o piu superfici di rotazione


This research concerns the drawing up of 3d descriptive geometric procedures aimed to determine the geometric loci of the points equidistant from two or more quadrics

la ricerca riguarda la stesura di procedimenti geometrici descrittivi 3d atti alla determinazione dei luoghi geometrici dei punti equidistanti da due o piu superfici di rotazione

le bisettroide di due superficie di rotazione: cono e clindro
(السطح المنصف لسطحين دائريين: مخروط و اسطوانة)

le generatrici della bisettroide in questione si ottengono nella maggior parte dei casi come luogo geometrico dei punti equidistanti da due coniche, eventualmente degeneri. il modo più semplice per ottenere tali coniche consiste nel utilizzare dei piani secanti passanti per il vertice del cono. ciascun dei quali seziona il cono secondo due generatrici, e seziona il cilindro nella maggior parte dei casi secondo un ellisse. il luogo geometrico dei punti equidistanti dalle generatrici del cono e dalle ellissi del cilindro sono le generatrici della bisettroide. Tale luogo geometrico nella maggior parte delle citate coniche e' una parabola.

bisettroide di due superficie di rotazione: cono e clindro
 السطح المنصف لسطحين دائريين: مخروط و اسطوانة

come abbiamo detto : il luogo geometrico dei punti equidistanti dalle due date superfici di rotazioni rappresenta le generatrici della bisettroide cercata. ma poiché esistono due e non una parabole come luoghi geometrici dei punti equidistanti da un retta (sezione del cono) e da un ellisse (sezione del cilindro), allora sono due le bisettroidi cercate

esistono due bisettroidi tra le due superfici di rotazione date : cono e cilindro

 

la giustificazione spaziale della parabola come luogo geometrico dei punti equidistanti da una retta e una circonferenza

prima di verificare che la bisettroide ottenuta come luogo geometrico dei centri delle sfere tangenti due superfici di rotazione (in questo caso cono e cilindro) sia paraboloide iperbolico (seguendo il suggerimento del prof. Reccardo migliari), . devo necessariamente ricordare che sezionando il paraboloide iperbolico con dei piani perpendicolare al suo asse si ottengono delle parabole, e con dei piani paralleli all'asse si ottengono delle iperboli. inoltre il paraboloide iperbolico è anche una superficie doppiamente rigata. per cui per ogni suo punto passano due rette appartenenti per intero alla stessa superficie. quindi possiamo dire che se si va ad eseguire delle sezioni piane sulla detta bisettroide, e non si ottiene come risultato delle sezioni delle rette, parabole o iperbole, significa che la bisettroide non e' un paraboloide iperbolico ? 

https://www.researchgate.net/project/Geometric-Loci/update/5ccade0c3843b01b9b9dadb1?replyToId=5ccd4d3a3843b0b9825111d4

sezioni parabolici ed iperbolici della bisettroide 

nel disegno di sinistra sono dati rispettivamente la prima proiezione di un cono di rotazione K ,
e la seconda proiezione di K e di una sfera tangente K.
Si vuole determinare la prima proiezione di una delle due sfere tangente K

determinare una sfera di raggio assegnato in modo che sia  tangente un cilindro ed un cono in una generatrice data del cilindro 

تحديد الكرة بنصف قطر معلوم بحيث تكون متماسة لسطحين دائريين: مخروط واسطوانة. وبشرط مرور الكرة برأس المخروط
 Determinare la sfera di raggio assegnato tangente un cilindro ed un cono. Nella condizione che passi la sfera per il vertice del cono.

Se il luogo geometrico di tutte le sfere tangenti due superfici di rotazioni intersecanti, e' simile alla loro curva d'intersezione, allora come sara il luogo geometrico in assenza d'intersezione ?

Il luogo geometrico dei centri delle sfere tangenti due superfici di rotazioni non intersecanti tra loro
 المحل الهندسي لمراكز الكرات المتماسة سحطين دائريين غير متقاطعين فيما بينهما 

In questo modo sarebbe interessante poter modellare la superficie di un progetto architettonico come luogo geometrico di due o più superfici di rotazione, eventualmente degeneri in superficie piana ...

Nel caso in cui le due superficie non sono intersecanti tra loro, si ha che ciascuna generatrice della bisettrice cercata e' una quartica monogrammica simile alla quartica che si ottiene quando si costruiscono le superfici parallele alle due superficie di rotazione date, di una medesima distanza. inoltre si fa notare che la citata quartica si degenera in un punto quando le dette due superfici parallele sono tangenti tra loro.

la domanda iniziale

determinare una sfera tangente due superfici di rotazione: cono e clindro, nella condizione che passi per un punto P dato appartenente ad una generatrice g del cilindro ( o ad una generatrice del cono)

Risposta

il luogo geometrico dei centri delle sfere che soddisfano tale condizione puo essere una parabola .

quindi esistono infinite sfere che passano per P.

la soluzione consiste nel determinare la bisettrice delle due superfici , ovvero la superficie che funge da luogo geometrico dei centri delle sfere tangenti tali superfici,  e poi di condurre per P la retta r perpendicolare  alla superficie del cilindro. dove la retta r incontra la superficie della bisettroide, si ha il centro della sfera passante per P e tangente le superficie date.

Quindi senza la determinazione della bisettroide non sono riuscito a determinare la sfera passante per P e tangente le due superfici date.

costruzione di due rigate che hanno in comune una quartica monogrammica che funge da luogo geometrico dei centri delle sfere uguali tra loro e tangenti due superfici di rotazione: cono, cilindro.

nella figura allegata, sono  stati costruiti due superfici rigate che hanno in comune una quartica monogrammica che funge da luogo geometrico dei centri di sfere uguali tra loro e che tangono le due superfici di rotazione date: cono e cilindro. le generatrice delle due rigate sono perpendicolari rispettivamente alla superficie del cono e a quella del cilindro

le due rigate ottenute come sopra

Superfici di raccordo tangenziale di tre superfici di rotazione

la modellazione geometrica descrittiva di una Superficie di raccordo tangenziale di tre cilindri di rotazione uguali tra loro ed aventi i propri assi coincidenti con gli spigoli di un tetraedro

sono evidenziatati maggiormente le linee di costruzione del superficie ottenuta sopra

la fase preliminare della determinazione della superficie di raccordo tangenziale (diretto, ed inverso) tra tre coni di rotazione

Superfici di raccordo tangenziale (diretto ed inverso) di tre cono di rotazione

Prendendo in considerazione tre coni di rotazione non corrispondenti tra loro, la questione di raccordo diretto diventa laboriosa. invece per quanto riguarda il raccordo inverso, non sono riuscito ancora a determinarlo 🤨

verificando la curva ottenuta (colore blu) che funge da luogo geometrico dei centri delle sfere tangenti tre coni non corrispondenti si ha' una curva sghemba e non piana

la determinazione delle due superfici di raccordo tangenziale (diretto ed inverso) tra tre cono di rotazione non corrispondenti tra loro

Sono visualizzati di più le linee di costruzione del risultato sopra

Raccordo tangenziale tra tre cilindri di rotazione non intersecanti tra loro.
anche in panorama

in trasparenza

analogamente alle superfici rigate, per determinare una superficie di raccordo tangenziali vi servono tre direttrici, che in questo  caso sono un punto, una retta ed un piano

https://www.researchgate.net/project/Liquid-Architecture-in-virtual-space

https://isawi.blogspot.com/2019/04/luoghi-geometrici.html

analogamente ad un triangolo, dove esiste l'incentro e il circocentro, anche per un piramide triangolare R, esiste nello spazio  l'ncentroide e il circocentroide di una piramide triangolare R, che sono rispettivamente i centri di due sfere, una tangente gli spigoli di R e l'altra tangente le facce di R. e poiché la piramide triangolare e' composta da 4 angoloidi triedrici, per cui e' sufficiente determinare, come e' stato parzialmente  illustrato nel caso allegato,   i luoghi dei centri delle sfere inscriventi e quelli circoscriventi ciascun di tali angoloidi. e poi si va a determinare rispettivamente i loro punti d'intersezione per avere i cosiddetti incentroide e circocentroide di una piramide triangolare

saved to tangenza in Descriptive Geometry

1

Geometric Loci | Hasan Isawi | 14 updates | Research Project.

Dati 4 punti non appartenenti ad un stesso piano si ha una piramide triangolare K. l'incentroide di K si determina come punto comune alle bisettrici dei 4 angoloidi formanti K. e quindi tale punto rappresenta il centro della sfera tangenti tutte facce di K

Determine circumscribed sphere of an arbitrary tetrahedron, or in other words determine the sphere passing through 4 points not belonging to the same plane
la sfera individuata da 4 punti non appartenenti allo stesso piano
Analogamente al fatto che tre punti non allineati individuano una circonferenza, si può dire la stessa cosa nello spazio quando sono dati 4 punti non appartenenti allo stesso piano individuano una sfera.
poiché 4 punti non appartenenti allo stesso piano individuano un tetraedro, allora il centro di tale sfera rappresenta l'incentroide del tetraedro 
https://www.researchgate.net/project/Geometric-Loci

luogo geometrico dei punti di tangenza di superfici superfici con due date superfici di rotazione generiche tra loro

luogo geometrico dei centri due sfere tangenti a due sfere interne tra loro

out of equator: determinata la quinta sfera tangente a 4 sfere tangenti tra loro

solo sul bordo altrimenti tre a tre

iperbole come conica di tangenza inversa tra due coniche generiche

la ricerca si sta volgendo ad un bel termine ☺️
intanto si può dire che lavorando nel piano forse si può risolvere un solo problema ed un solo caso, e poi ripetere la soluzione in modo meccanico, ma solo ritornando allo spazio alle origine delle figure che hanno prodotto tali proiezioni, che si può generalizzare il problema e risolvere la maggior parte dei casi . quindi si può dire che la giustificazione spaziale delle cose e' come uscire dalla caverna platonica
الانشاءات الهندسية بين الاسقاطات قد تحل مسألة معينة وفي حالة واحدة فقط، وبعد ذلك يمكن تكرار الحل ميكانيكيا. ولكن من خلال العودة إلى أصل الاشكال التي أنتجت تلك الاسقاطات، من الممكن تعميم المسألة وتبرير مجموعة كبيرة من الحالات. ولذلك يمكن تشبيه التبرير الفراغي بعملية الخروج من الكهف الأفلاطوني😉

Invece di avere i soliti applicativi con limitati operazioni di montaggio e smontaggio,
ce un spazio geometrico infinito tutto .da scoprire. 

Tre fasci proiettivi che hanno in comune una stessa conica

interruzione primo semestre 2019

il luogho dei centri delle sfere tangenti due rette ed una sfera

Superficie di raccordo tangenziale tra una sfera e due cilindri circolari

-----------------------------------End