Modellazione geometrica di un museo-نمذجة هندسية وصفية لمتحف الموسيقى

Alisawi HomePage / Architettura 3d /

pagina in costruzione

---

UNIVERSITA' DEGLI STUDI DI ROMA "LA SAPIENZA" FACOLTA' DI ARCHITETTURA "VALLE GIULIA"
Studente Costanza Francavilla 2003 - 2004
01	02	03
04	05	06
La modellazione 3d sono stati elaborati  in AutoCAD 2004

---

Corso individuale di AutoCAD 2d 3d in 20 ore
Architetto. Isawi 
- Roma - Cell. 3285412431

---

START

Isawi Home Page

_

السطح الاسقاطي- Superficie Proiettiva

في الهندسة الوصفية، السطح الاسقاطي يتولد كحزمة من الخطوط التي يمكن ان تشترك بنقطة نهائية ( كم هو رأس الهرم اوالمخروط)  او لانهائية (كما هو اتجاه احرف المنشور او اتجاه رواسم الاسطوانة). تقاطع حزمة الخطوط مع أي مستوى يمكن ان ينتج قاعدة السطح الاسقاطي. هذه القاعدة يمكن ان تكون مضلع او منحنى. وفقط في الحالة التي يكون فيها هذا المستوى عمودي على المحور المحتمل للحزمة, المقطع يسمى مقطع قائم. مثلا المقطع القائم لحزمة مكونة من ثلاثة خطوط يكون مثلث, ومحور الحزمة يمر بنقطتين هما: الاولى مركز الحزمة  والثانية مركز الدائرة المحاطة بالمثلث .

cupola con Petali a coni ellittici

Isawi HomePage / Geometria / cupola con Petali a coni ellittici Modellazione solida  di una cupola a base ottagonale ottenuta come intersezione di coni ellittici disposti in modo simmetrico rispetto al centro di una sfera delta. Le aperture presenti nella cupola, chiamati "petali" per la loro forma, sono due archi di circonferenza che sono  ottenute, ciascuno, come intersezione di un cono ellittico con  la sfera delta. Ciascun cono ellittico ha come propria sezione retta un ellisse, il quale appartiene ad un piano meridiano passante per una diagonale del ottagono di base. gli assi di tale ellisse sono, rispettivamente, quello maggiore è uguale alla diagonale del ottagono,quello minore è uguale al raggio della sfera delta.    proiezioni ortogonali (Monge) e assonometrie ( visti dal basso e dall'alto)   proiezioni ortogonali (Monge) e assonometria  Come determinare delle circonferenze come sezioni di un cono ellittico Indice Home creata il 30-09-2005

Superficie di raccordo tangenziale tra due coni circolari ad assi incidenti

Isawi HomePage / Geometria Descrittiva / Tang03

---

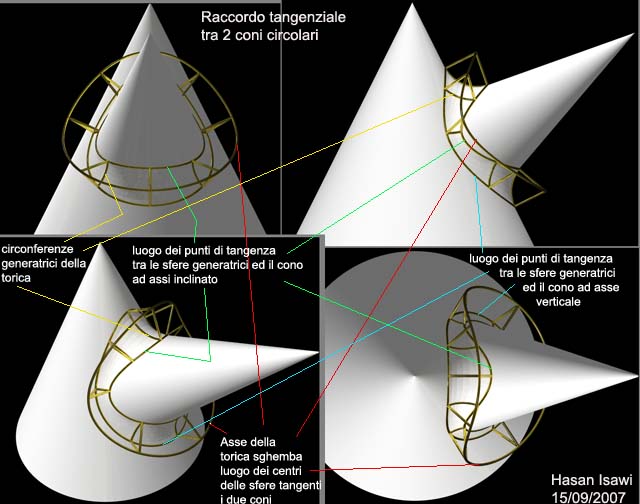
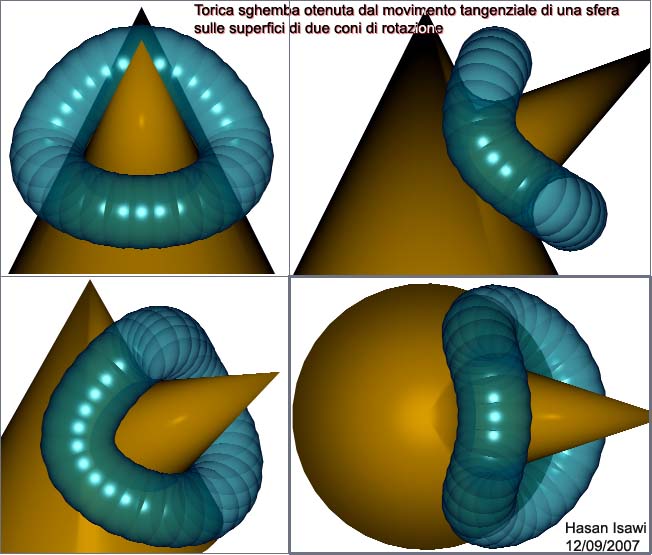
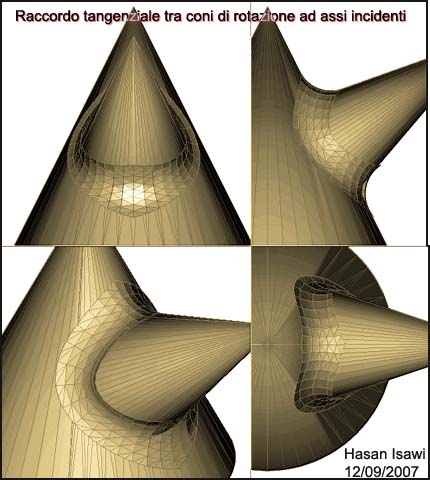
Superficie di raccordo tangenziale  tra due coni circolari ad assi incidenti

01- Proiezioni mongiane e una vista assonometrica

02

altri Casi di raccordi tangenziali tra superfici di rotazione
tra toriche ad assi //
tra toriche uguali e con assi perpendicolari tra loro
tra un toro con un cilindro ad assi paralleli
tra un toro con un cono ad assi incidenti
di un cono e un cilindro ad assi perpendicolari  ||

 

Home

Raccordo tangenziale tra ellissoide

Isawi HomePage / Geometria Descrittiva / Tang04

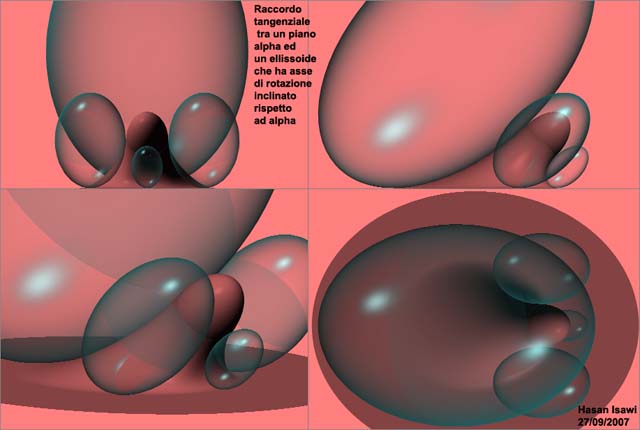
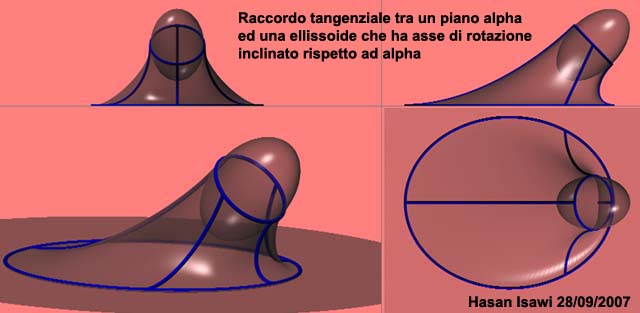
Raccordo tangenziale tra ellissoide K e piano alpha. In cui è stabilito che l'asse di K è inclinato rispetto ad alpha

la superficie di raccordo appartiene ad una toro ellittico a generatrice circolare variabile

Altri casi di superfici di Raccordo tangenziale

di un angoloide quadrico con una quadrica di rotazione
tra superfici di rotazione
tra toriche ad assi //
tra toriche uguali e con assi perpendicolari tra loro
tra un toro con un cilindro ad assi paralleli
tra un toro con un cono ad assi incidenti
di un cono e un cilindro ad assi perpendicolari  ||

 

Home

_

Toro ellittico

Isawi HomePage / Geometria / Movimento / torroide ellittico:
ottenuto da una

Trasformazione ciclica di un ellissoide di rotazione E in modo che risulti sempre tangente a due ellissoidi F ed G. Stabilito che F e G sono omotetiche e concentriche tra loro.

Nota: l'asse di rotazione delle due ellissoide è quello maggiore

Finalità didattica Determinare le coniche tangenziali di  minima e di massima distanza*  intercorrenti tra due date coniche complanari * In considerazione del fatto che tra i possibili coniche tangenti a due coniche date Delta e Fi, vi esistono due sole che hanno, rispettivamente, minima e massima lunghezza rispetto alle coniche date Delta e Fi.. Dalle reciproche combinazioni dei tipi e di posizioni di  due coniche date ed escludendo quelli in cui tali coniche sono entrambe degeneri, nascono in generale, i seguenti i casi:  - coniche omotetiche: sono inclusi i casi in cui le due coniche date sono: - simili e congruenti. - solo simili: inclusi i casi in cui una delle due coniche è degenere. - Coniche generiche

Cono ellittico tangente un ellissoide di rotazione.

forse si avvicina la soluzione di come determinare una sezione retta di un cono generico

---

Indice

Home

creata il 17-04-2006

---

تقاطع مخاريط

شكل1: تقاطع بين مخروطين, في هذة الجاة المستويات المساعدة القاطعة المخروطين تمر بالخط المار بقمتيهما

تقاطع مخاريط

شكل1: تقاطع بين مخروطين, في هذه الحالة المستويات المساعدة القاطعة المخروطين تمر بالخط المار بقمتيهما


التقاطع بين المخاريط يعتبر في الهندسة الوصفية واحد من حالات التقاطع بين الأسطح المسطرة [1] . وبما أن الأسطوانة هي حالة استثنائية للمخروط، فيمكن سرد حالات التقاطع كما يلي :

• بين مخروطين (شكل1)
• بين أسطوانتين
• بين مخروط واسطوانه

في جميع الحالات المذكورة يمكن إيحاد منحنى التقاطع بين اثنين من الأسطح المخروطية، باستخدام عدد كاف من المستويات المساعدة المشتركة بالخط المار بقمتي السطحين والقاطعة او الماسة لسطحيهما.

وفقا للحالات الفردية المذكورة أعلاة، الخط المار بقمتي السطحين، يمكن أن يكون :

• خط نهائي , عندما السطحين يكونا مخروطين (أو مخروط واسطوانه) ، أي ان الخط المشترك للمستويات المساعدة يمر بنقطتين . أللتي يمكن ان يكونا نقطتين نهائيتين في حالة المخروطين (شكل1), ونقطه نهائية والأخرى لانهائية في حالة المخروط والأسطوانة. في هذه الحالة الأخيرة الخط المعني يمر بقمة المخروط ويكون موازي لمحور الأسطوانة.
• خط لانهائي، عندما يكون هناك أسطوانتين. في هذة الحالة المستويات المساعدة تكون موازية لمحوري الأسطوانتين.

مصادر
^ تقاطع أسطح برواسم مستقيمة (باللغة الايطالية]

طالع ايضا
تقاطع


وصلات خارجية
Casi d'intersezione tra Superfici di rotazione