=====================================================================
يعتبر السطح سطحا مسطرا (Surface Ruled) إذا تمكنا من رسم خط مستقیم في كل نقطة من ھذا السطح بحیث یقع بأكمله على نفس السطح.
أشھر الأمثلة على السطوح المسطرة ھو السطح المستوي والسطح المخروطي (بما في ذلك الأسطوانة كحالة خاصة من المخروط).
وتعد ھذه الحالة الأخیرة حالة خاصة من السطوح الثنائیة (والتي تشتمل أیضا على السطح المكافئ الزائدي والسطح الزائد بطیة واحدة والسطح المخروطي ذو الدلیل الناقصي.
ومن الأمثلة الأخرى على ذلك السطح شبه المخروطي القائم واللولباني.
نطلق على سطح ما بأنھ سطح مزدوج التسطر إذا استطعنا أن نرسم من كل نقطة على السطح مستقیمین یقعان بأكملھما على نفس السطح. المستوى والسطح المكافئ الزائدي (الشكل 1) والسطح الزائد () ھم السطوح الثنائیة الوحیدة التي تدخل ضمن ھذا النوع من الاسطح مزدوجة التسطر.
السطح القابل للفرد (أوالبسط) -هو السطح الذي یمكن بسطه على مستوى دون انكماش أو تمدد
أشھر الأمثلة على السطوح المسطرة ھو السطح المستوي والسطح المخروطي (بما في ذلك الأسطوانة كحالة خاصة من المخروط).
وتعد ھذه الحالة الأخیرة حالة خاصة من السطوح الثنائیة (والتي تشتمل أیضا على السطح المكافئ الزائدي والسطح الزائد بطیة واحدة والسطح المخروطي ذو الدلیل الناقصي.
ومن الأمثلة الأخرى على ذلك السطح شبه المخروطي القائم واللولباني.
نطلق على سطح ما بأنھ سطح مزدوج التسطر إذا استطعنا أن نرسم من كل نقطة على السطح مستقیمین یقعان بأكملھما على نفس السطح. المستوى والسطح المكافئ الزائدي (الشكل 1) والسطح الزائد () ھم السطوح الثنائیة الوحیدة التي تدخل ضمن ھذا النوع من الاسطح مزدوجة التسطر.
السطح القابل للفرد (أوالبسط) -هو السطح الذي یمكن بسطه على مستوى دون انكماش أو تمدد
 |
| هندسة وصفية ، تطبيق مفهوم السطح المسطر لتصميم مكتبة |
 |
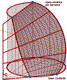
| تسطر مزدوج لسقف مكافئ زائدي - خطوط محورية work in progress 3 http://isawi.blogspot.com/2018/06/blog-post.html |
Paraboloide iperbolico
مقترح لانشاء عريشة على شكل سطح مكافئ زائدي خلال مساق مشغل مباني
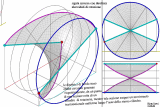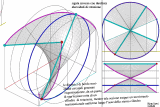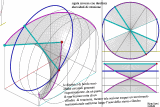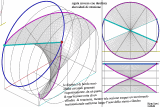
السطح المكافئ الزائدي (paraboloid hyperbolic) يتشكل من حركة خط يدعى راسم (generatrix ) على طول خطين متخالفين، وكل منهما يسمى دليل (directrix )، وعند قطع السطح بمستوى رأسي يمكننا الحصول على قطع مكافئ ، أما عند قطعه بمستوى أفقي فيمكننا الحصول على قطع زائد
 |
| work in progress - 1 paraboloide iperbolico da realizzare con riutilizzo Di Bottiglie Di Plastica |
 |
| work in progress - 2 |
 |
| Hide |
 |
| Render |
 |
| Shade |
 |
| fase finale della rigatura doppia della paraboloide iperbolica in questione http://isawi.blogspot.com/2018/06/blog-post.html — at Paraboloide iperbolico . |
 |
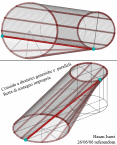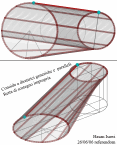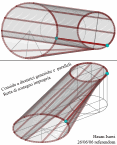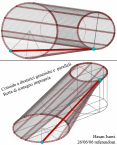
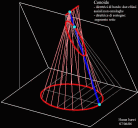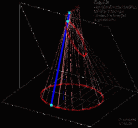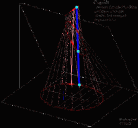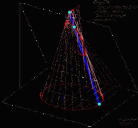
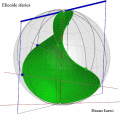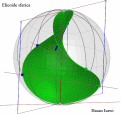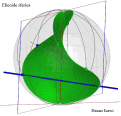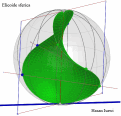
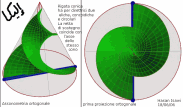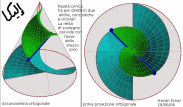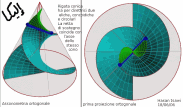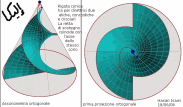
| Superficie rigata ottenuta dalla Trasrotazione di un segmento retto lungo una circonferenza ed una retta verticale passante per il centro della stessa circonferenza |
------------------------------
 |
la superficie rigata illustrata ha come direttrici un punto ed una elicoide sferica che e' stata ottenuta come somma di punti d'intersezione di una sfera con una retta. Il quale esegue un movimento trasrotazionale regolare avendo un punto fisso nel centro della sfera
|
tra ellissi omotetiche
ارشيف
22/08/2006 - pagina in costruzione
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
* Riga
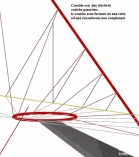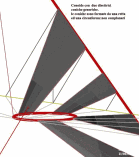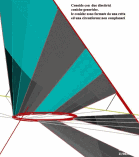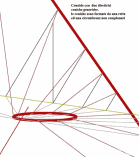
ta quadrica * Rigata genercia * esplorazione le Rigate sono ottenute dal movimento di una retta, detta generatrice, lungo tre rette, complanari due a due, dette direttrici. Al variare delle reciproche posizioni di tali direttrici, si hanno diversi tipi di rigate. Per costruire una rigata occorre assegnare un quadrilatero sghembo abcd. e poi scegliere due lati opposti a c come generarci e gli altri lati b d come due delle tre direttrici occorrenti a tale costruzione. Si tiene presente che due rette sghembe individuano in tutti i casi due piani tra loro paralleli, per cui le rette direttrici b d possono individuare alpha e beta come due di tali piani. Di consegue, la terza direttrice si può determinare come retta sostegno di una fascio di piani: che passa per le generatrici a c ed ha giaciture perpendicolari ai piani individuati dalle direttrici b d. Nel caso in cui i lati abcd, del quadrilatero individuano due piani paralleli tra loro, si ha come terza direttrice una retta improria: sostegno di una fascio di piani paralleli.  | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Per ottenere una una superficie doppiamente rigata, si può considerare, rispettivamente, che le direttrici a ed b siano generatrici e che due generatrici c ed d siano direttrici. in questo modo la rigata viene detta Parabolide iperbolico | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
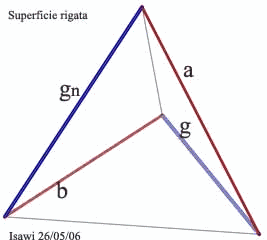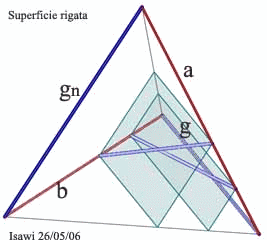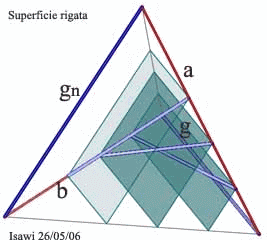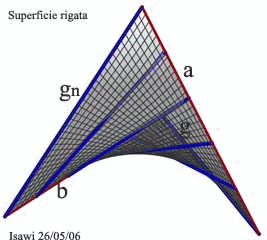
stabilito di costruire una superficie rigata delimitata da un quadrilatero sghembo che ha come propri lati: quattro spigoli di un tetraedro regolare ( vedi figura accanto. Inoltre, si stabilisce che due spigoli g gn, siano le generatrici, e che gli altri due spigoli a, b siano due delle tre direttrici. La terza retta direttrice u si individua determinando la retta d'intersezione di due piani. I quali passano, rispettivamente per le generatrici g ed gn ed hanno giacitura perpendicolare a quella dei piani paralleli individuati dalle due rette direttrici a ed b.
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Approssimazione di una Rigata solida | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Poiché due rette sghembe individuano, in tutti i casi, un tetraedro, si può approssimare una superficie rigata K con un numero limitato di tetraedri che vengono individuati dalle generatrici sghembe di tale superficie. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Osservazione : rigate e software La tecnica che viene adottata dai software dì grafica 3D per creare una superficie delimitata da un quadrilatero sghembo, è quella di dividere i lati opposti in segmenti uguali e di congiungere gli estremi di tali segmenti. Poiché una superficie rigata ha la proprietà di avere le proprie generatrici appartenenti ad un stesso fascio di piani ( vedi figura sotto a destra), per cui la detta tecnica ci porta ad avere una superficie che non può essere classificata come Rigata. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
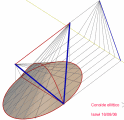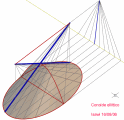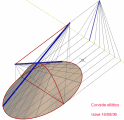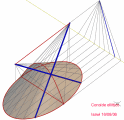
i casi affrontati riguardano le rigate che hanno come direttrici di bordo le seguenti coniche
- due ellissi corrispondenti * - cono quadrico
* ellissi corrispondenti: sezioni piane dello stesso cono quadrico. ovvero, le coppie di punti corrispondenti, delle due coniche devono essere allineai con un stesso punto: centro della prospettività coincidente con il vertice del possibile cono quadrico. altrimenti si ha un conoide che si differenzia dal cono quadrico nel fatto che vine generato con multiplici stelle di rette, tutte con i centri appartenenti ad una stessa retta.
- due ellissi assiali - conoide
- due ellissi generiche non assiali - conoide
- una retta ed un ellisse - superficie: conoide - sostegno: una retta
- una parabola ed un ellisse - conoide
Viene definita tale quando viene generata da una sola retta che scorre lungo tre direttrici coniche, eventualmente degeneri.
Vediamo di esplorare i possibili tipi di "rigate quadriche"
 |
Nella figura è rappresentata un rigata quadrica che ha come direttrici due coniche involutorie
|
- rigate quadriche
Rigate singole
- rigate generiche
Rigata doppie
Le rigate degeneri vengono individati da un triangolo
con direttrici coniche avente come sostegno una conica degenere
a secondo della complanarità e del tipo di direttrci le rigate in
* piane, ha direttrici individuati da un triangolo
* rigate, ha per direttrici tre rette
** rigate coniche
** rigate generiche
* coniche: individuate da un quadrilatero sghembo
* generiche
* * le rigate individuate da un quadrilatero sghembo
In questo caso la superficie rigata si ottiene dall'intersezione tra due coni quadrici, incluso il cilindro come caso particolare di cono, con la condizione che abbiano una conica in comune, è un tipo di rigata singole, per cui, ha come direttrice due coniche ellittiche. I quali si ottengono ,rispettivamente, come intersezione delle generatrici complanari di tali coni quadrici.
* Quadrilatero sghembo: si differenzia dal quadrilatero piano per non avere tutti i punti appartenenti ad un stesso piano.
altre tipi di superfici escluse dalla categoria delle rigate ( argomento da approfondire
 | ||||||||
| Arcuata (wait) |
| |  |
----------------------------
01/07/2006
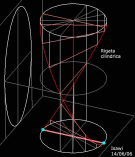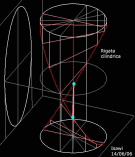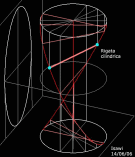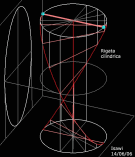
Elicoidali
Esse sono generate dal movimento di una retta g lungo tre direttrici, in cui una di tali direttrici, come gli altri tipi di rigate: quadriche e conoidiche, è la cosidetta retta di sostegno, le altre due direttrici, nel caso delle rigate elicoidali, sono formati da due eliche che possono essere, rispettivamente, coniche, cilindriche e toriche.
| Elicoide sferica Rigata a direttrici elicoidale sferiche |  |
| Elicoide sferica Rigata a direttrici elicoidale toriche di rotazione |  |
| Elicoide cilindrica Rigata a direttrici elicoidale cilindriche di rotazionele direttrici di bordo sono eliche generate dal movimento di un punto di una sezione retta di un cilindro di rotazione, mentre tale sezione esegue un movimento trasrotatorio uniforme lungo l'asse dello stesso cilindro |  |
| rigata conica a direttrici elicoidali asimmetriche (2)le direttrici di bordo sono due eliche asimmetriche, ottenute dal movimento di due punti d'intersezione di un cono quadrico K con una retta r , mentre questa esegue una trasformazione trasrotazionale costante lungo l'asse dello stesso cono. Le due eliche sono asimmetriche per il fatto che la trasformazione di r avviene su piani non paralleli a quello di una sezione retta dello stesso cono K. |  |
| caso (2): la generatrice è una retta inclinata rispetto al piano della sezione retta di un cono di rotazione | |
| rigata conica a direttrici elicoidali simmetriche (1)la generatrice è una retta incidente un cono, sia circolare, sia ellittico ed parallela alla sezione retta dello stesso cono le direttrici di bordo sono due eliche asimmetriche, ottenute dal movimento di due punti d'intersezione di un cono quadrico K con una retta r, mentre questa esegue una trasformazione trasrotazionale costante lungo l'asse dello stesso cono K. Le due eliche presentano un caso di simmetria centrale, dovuto al fatto che la trasformazione di r avviene su piani paralleli a quello di una sezione retta dello stesso cono K. - retta di sostegno: coincide con l'asse di un cono circolare |  |
| icaso (1): la generatrice è una retta parallela al piano della sezione retta di un cono di rotazione | |
| rigata cilindrica circolare, si ottiene dalla trasformazione geometrica tra due segmenti sghembi A_B, A'_B' , nella condizione in cui tali estremi rimangono, durante il loro movimento, vincolati ad altrettanti punti di una sezione piana di un cilindro di rotazione. |  |
 | |
روابط خارجية
- le quadriche in architettura
http://slideplayer.it/slide/11929372/
| _ | Superfici rigate
www.federica.unina.it/architettura/applicazioni-di-geometria-descrittiva/superfici-rigate/
Si definiscono rigate le superfici generate dal movimento di una retta nello spazio secondo una determinata legge di moto.Le rette che definiscono la superficie si dicono generatrici mentre si definisce direttrice una qualsiasi curva appartenente alla superficie che abbia in comune con ciascuna generatrice un solo punto.Le rigate possono essere distinte in:sviluppabili: quando due generatrici consecutive sono sempre complanari e quindi incidenti, e la superficie può essere distesa su un piano;non sviluppabili: quando due direttrici sono sghembe e la superficie non può essere distesa su un piano.Assegnate tre curve sghembe nello spazio, che si assumono come direttrici, si può definire rigata generica la superficie generata dal moto di una retta che si appoggia alle tre direttrici.Se una delle tre direttrici è una retta impropria la rigata si dice a piano direttore, infatti tutte le generatrici per intersecare la retta impropria saranno parallele ad un piano detto appunto piano direttore.Le rigate possono essere anche classificate in funzione dell’ordine, in particolare sono superfici del secondo ordine e quindi quadriche rigate: il cono quadrico; il cilindro quadrico; l’iperboloide ad una falda; il paraboloide iperbolico.
Rigata generica
| |
ليست هناك تعليقات:
إرسال تعليق