|
|
|
|
|
ASSONOMETRIA
- Generica
La proiezione assonometrica si basa sulla proiezione di un oggetto 3dimensionale
con la direzione di un punto improprio, detto
centro di proiezione, su un piano, chiamato quadro o piano di
proiezione). In questo metodo, come negli altri metodi (proiezione ortogonale e prospettiva),
si deve valere la corrispondenza
biunivoca tra l'oggetto e la sua immagine assonometrica, in modo da restituire le caratteristiche geometriche e la posizione
di tale oggetto
nello spazio.
A tale fine è stabilito un sistema di riferimento
ausiliario costituito da tre piani xy. xz, yz, tra loro ortogonali, e
Sui quali
si determinano le proiezioni ortogonali dei punti e delle rette che
definiscono l'oggetto.
Il metodo delle proiezioni assonometrica ha la
proprietà di: - mantenere inalterato il rapporto di riduzione tra un
segmento e la
sua immagine assonometrica, qualunque sia la posizione, purché si
mantenga la stessa
direzione di proiezione; - la conservazione del parallelismo (rette
paralleli hanno immagini parallele).
La direzione del centro di proiezione rispetto al
quadro, determina una classificazione nel metodo delle proiezioni
assonometrica
(P.A.), se l'angolo che forma la direzione del centro di proiezione con
il
quadro è uguale 90° , l'assonometria viene detta "Ortogonale" fig.1\a., altrimenti l'assonometria viene
chiamata "obliqua" fig.1\b.
Ortogonale (fig.2)
Stabilito che si voglia proiettare, con una direzione C¥ perpendicolare al quadro p,
tre assi triortogonali x, y, z, ed, fig inoltre, si considera che a tali assi appartengano tre
segmenti con uguale lunghezza (segmenti unitari) ux, uy, uz, con in comune il punto origine O, si ha:
- x', y', z', proiezione assonometrica dei tre assi sul quadro, rette d'intersezione con il quadro dei tre piani proiettanti contenenti
rispettivamente detti assi
- O', proiezione assonometrica dell'origine O, coincide con l'ortocentro del triangolo delle tracce
L'inclinazione degli assi x,
y, z, rispetto al quadro determina un'uguale o differente riduzione dei
rispettivi segmenti unitari ux, uy, uz. Da questa considerazione
discende la seguente classifica dei tre tipi d'assonometria ortogonale.
1.
Isometrica:
gli
assi oggettivi x, y, z, formano con il quadro eguale angolo e da questo
discende che il triangolo delle tracce equilatero e i segmenti
unitari hanno lo stesso rapporto di riduzione ux'=uy'=uz'.
( vedi un esempio di rappresntazione in assonometria
isometrica))
2.
Dimetrica: due delle tre assi x, y, z, formano con il quadro eguale angolo e da questo
discende che il triangolo delle tracce isoscele e i segmenti unitari di quelle due assi hanno lo stesso rapporto di riduzione.
3.
Trimetrica:
tutte
le tre assi x, y, z, formano con il quadro diverso angolo e da questa
deriva che il triangolo delle tracce è scaleno ed il rapporto di
riduzione dei segmenti unitari ux, uy, uz, è tra loro differente.
Obliqua
La direzione del centro C¥ è inclinata rispetto al quadro p.
La posizione della terna degli assi x, y, z, determina i seguenti tre tipi d'assonometria obliqua:
1. Generica: se ciascuno dei tre assi interseca il quadro, gli assi possono, teoricamente, formare qualunque angolo con il quadro. - la
proiezione assonometrica dell'origine O non coincide con l'ortocentro del triangolo.
| 2. Cavaliera: quando si stabilisce che due assi sono coincidenti o paralleli al quadro, se gli assi sono xy (p1 l'assonometria è detta Cavaliera Militare (il suo l'impiego consente di disegnare la pianta in vera forma e misura), se invece sono x, z oppure y, z (rispettivamente p1, p2) a coincidere con il quadro, l'assonometria è detta Cavaliera Frontale (il suo impiego consente di disegnare il prospetto frontale in vera forma e misura). |  |
continua ....
Data
Creazione 1/10/1999
|
last update 05/05/2006 17:53 |
|
|
|
 |
Teorema di pholke (teorema fondamentale dell'assonometria)
assegnati sul piano di quadro tre segmenti unitari, Ux', Uy', Uz', aventi un estremo comune O'e lunghezza e direzione qualsiasi, esiste in ogni caso nello spazio un centro proiezione improprio, tale che sia possibile considerare i tre segmenti assegnati come proiezione da quel centro di tre segmenti uguali uscenti da un origine o, perpendicolare tra loro a due a due .
la dimostrazione di questo teorema è molto complesso ed è riportata in vari testi, tra i quali: Bompiani - geometria descrittiva per l'allievi di ingegnaria.
Rif.: lezioni ed esericizi di fandamenti e applicazioni di geometria descrittiva. - Lamberto nasini. - edizione Kappa
le figure del capitolo IV°, dalla N° 192 alla N° 269 sono stati elaborati al computer dall'arch. Isawi Hasan
- Consulta la voce assonometria di questa pagina:
http://members.xoom.virgilio.it/alisawi/geomtr.htm
continua ....
messaggio di richiesta:
> Salve sono un laureando in Architettura presso la
> facoltà Federico II di Napoli, vorrei sapere se ha
> qualche informazione da darmi riguardo il Teorema di
> Polke.
>
> Sicuro di una sua pronta risposta le porgo i miei
> più cordiali saluti.
>
> N.B. sarò lieto di mensionarla nella bibliografia
> della mia tesi di laurea.
>
> Biagio
> facoltà Federico II di Napoli, vorrei sapere se ha
> qualche informazione da darmi riguardo il Teorema di
> Polke.
>
> Sicuro di una sua pronta risposta le porgo i miei
> più cordiali saluti.
>
> N.B. sarò lieto di mensionarla nella bibliografia
> della mia tesi di laurea.
>
> Biagio
Data Creazione 03/04/2003 |
last update 28/09/2005 00:46 |
Assonometria isometrica ortogonale
From: "A D UrsoTo: < hasanisawi@hotmail.com
Date: Tue, 23 Jan 2001 21:27:42 +0100
Gentilissimo Architetto,
io sono una ragazza di 15 anni, frequento il Liceo Scientifico con la sperimentazione nella tecnologia. Nella mia sezione è di particolare importanza il disegno tecnico ed io poichè tra alcuni giorni devo consegnare un disegno di una proiezione assonometrica isometrica di un monolocale arredato io verrei chiederle un suo aiuto. Gentilmente potrebbe mandarmi la procedura con una e-mail?, Lo so è difficile, basta che me lo fa in piccole dimensioni giusto per avere un'idea.
Spero che potrà aiutarmi
La ringrazio anticipatamente
Distinti saluti
D'Urso Anellina.
salve Anellina
I seguenti link numerici sono riferiti alla procedura per la rapprsentazione di un volume in assonometria isometrica ortogonale.
buon studio
Hasan
-------------------
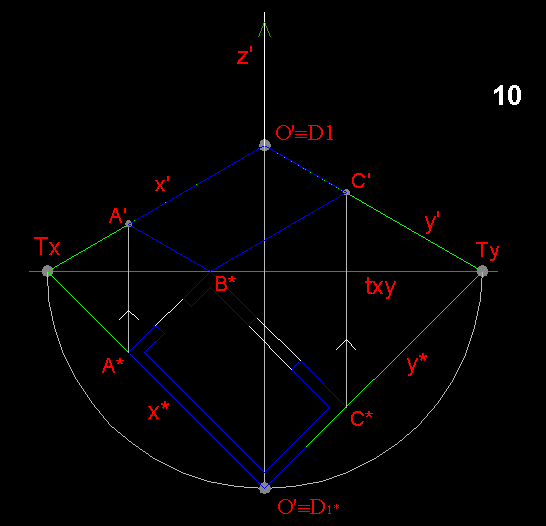
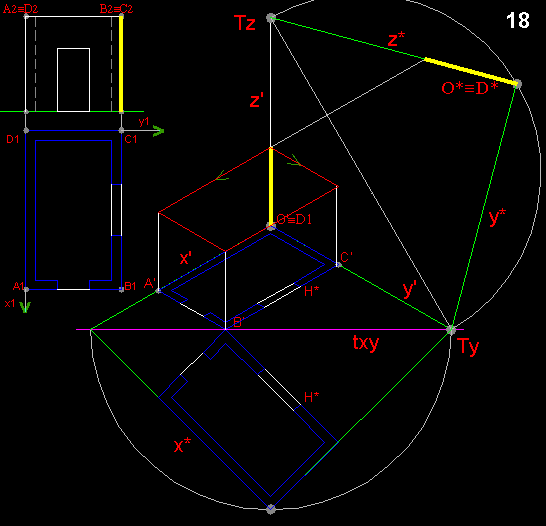
la corrispondenza omologica tra
le due figure, quella ribaltata e quella assonometria, consiste nell'allineare
i punti corrispondenti ( A*,A')
con il centro dell'omologia (la
direzione perpendicolare alla cerniera txy)
e nel fare incontrare le rette corrispondenti
(y*,y')
sull'asse dell'omologia, che in questo caso è la cerniera.si unisscono i punti C', A' con B* (in questo caso coincidente con B'), trovando la pianta del perimetro esterno.
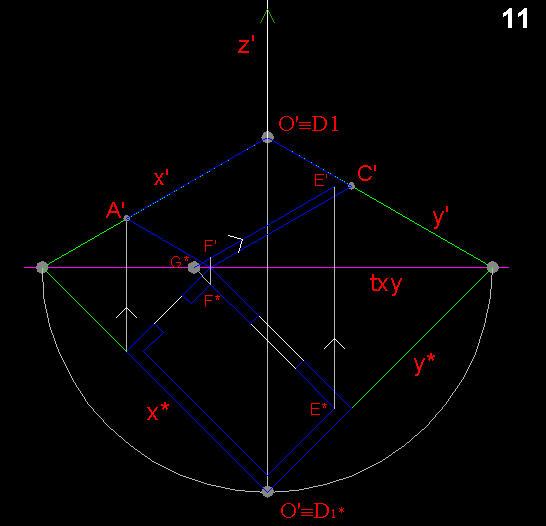
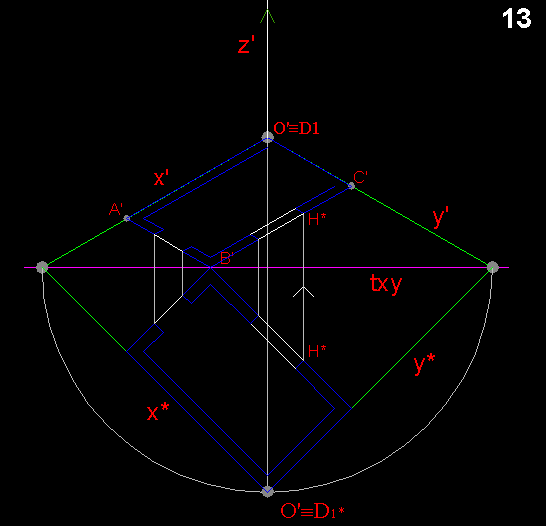
Si prolunga il lato E*, F* fina al punto G*, intersezione con la cerniera txy. I punti E', F' si trovano nei punti d'intersezione delle rette verticali, passanti per E*, F*, con la parallela ad x' passante per G*.
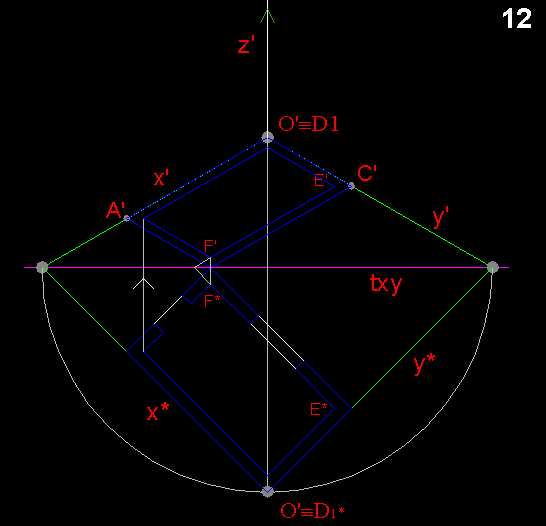
per esempio per trovare H', si traccia la perpendicolare a txy fino ad incontrare il segmento-immagine C'-B'
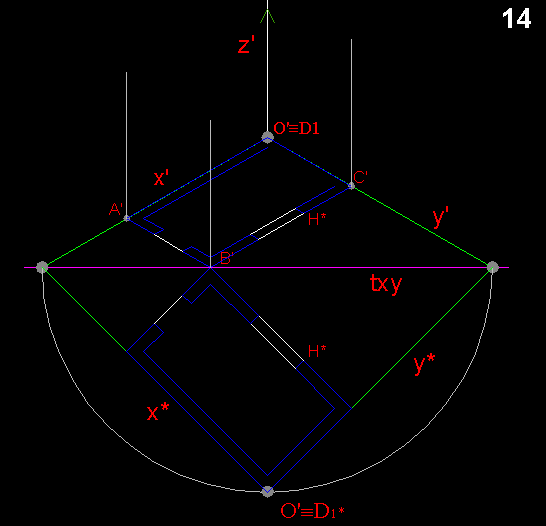
per trovare le riduzione delle proiezione assonometrica dei segmenti verticali,
occorre ribaltare, sul piano di proiezione, un piano verticale contenente l'asse z,
a tale fine utilizzeremo come piano
cartesiano yz e come cerniera, la sua traccia Tyz.
La retta Tyz è tacciabile unendo i punto Ty
con la direzione perpendicolare alla retta x'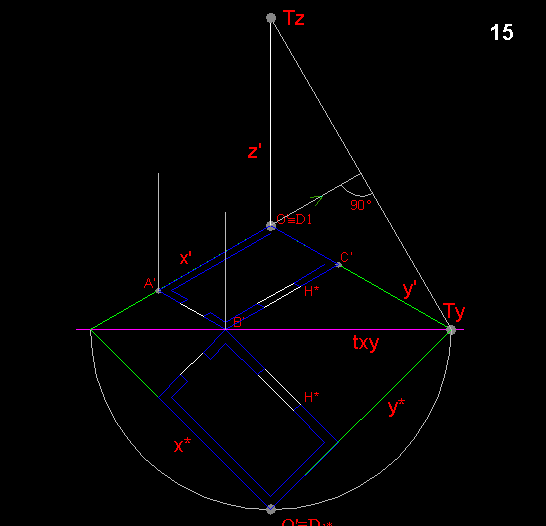
le vera misura dell'altezza del locale si prende dalla seconda
proiezione ortogonale e si mette su z*, per trovare
la rispettiva riduzione assonometrica si traccia la perpendicolare alla cerniera
tyz fino ad incontrare z'.
 |
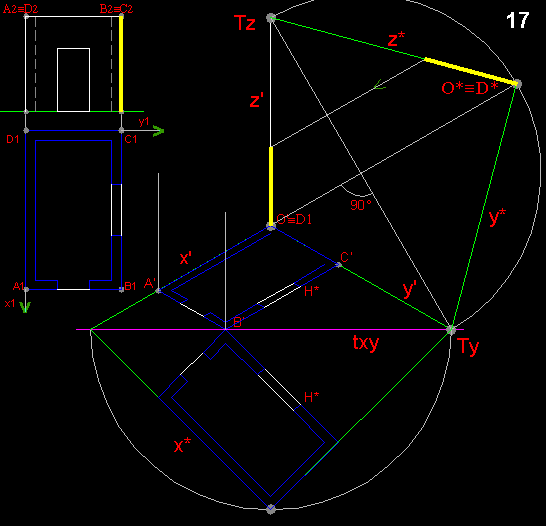Una volta trovata la riduzione assonometrica della altezza di un spigolo, in
questo caso è quello coincidente con z', si
procede a tracciare le rette parallele a x', y',
per completare il volume esterno.
 |
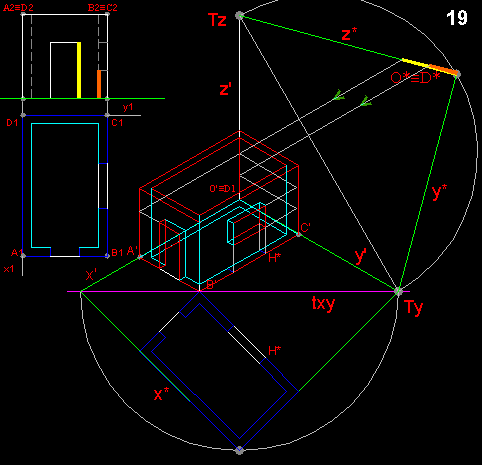
Si completa, tramite il parallelismo tra rette, l'immagine del volume interno.
Per trovare gli immagini dei segmenti verticali, rappresentanti in questo caso l'altezza della porta e della finestra, si procede con la stessa tecnica applicata precedentemente.
 |
ليست هناك تعليقات:
إرسال تعليق