بحث هذه المدونة الإلكترونية
14/11/2016
13/11/2016
Bisettrice di un angoloide triedrico- تحديد منصف زاوية صلبة
منصف زاوية صلبة ثلاثية السطوح
معلوم: ثلاثة مستويات α و β و γ.مطلوب: تحديد منصف الزاوية الصلبة المكونة من المستويات المعلومة
الخطوات
- - تحديد المستوى المنصف δ للزاوية الزوجية المكونة من المستويين α و β
- تحديد المستوى المنصف φ للزاوية الزوجية المكونة من المستويين α و γ
- تحديد خط التقاطع d بين المستويين δ و φ.
يمثل d الخط المنصف المطلوب للزاوية الصلبة المكونة من المستويات α و β و γ
وبالتالي فإن الخط d يمثل المحل الهندسي لمراكز الكرات المتماسة للمستويات المكونة الزاوية الصلبة
ملاحظة
- - تحديد المستوى المنصف δ للزاوية الزوجية المكونة من المستويين α و β
- تحديد المستوى المنصف φ للزاوية الزوجية المكونة من المستويين α و γ
- تحديد خط التقاطع d بين المستويين δ و φ.
يمثل d الخط المنصف المطلوب للزاوية الصلبة المكونة من المستويات α و β و γ
وبالتالي فإن الخط d يمثل المحل الهندسي لمراكز الكرات المتماسة للمستويات المكونة الزاوية الصلبة
ملاحظة
لتحديد المستوى المنصف لزاوية زوجية مكونة من مستويين α و β نتبع الخطوات التالية:
- تحديد خط التقاطع r بين المستويين α و β
- تحديد مستوى متعامد على الخط r ، والذي سيتقاطع مع α و β وفقا لخطين a و b.
- تحديد المنصف s للخطين a و b .
- تحديد المستوى المطلوب δ والذي يمر بالخطين r و s
يمثل المستوى δ المحل الهندسي لمراكز الكرات المتماسة المستويين α و β المكونين الزاوية الزوجية.
- تحديد خط التقاطع r بين المستويين α و β
- تحديد مستوى متعامد على الخط r ، والذي سيتقاطع مع α و β وفقا لخطين a و b.
- تحديد المنصف s للخطين a و b .
- تحديد المستوى المطلوب δ والذي يمر بالخطين r و s
يمثل المستوى δ المحل الهندسي لمراكز الكرات المتماسة المستويين α و β المكونين الزاوية الزوجية.
Tav. 08: Bisettrice di un angoloide triedrico |
|
last update 23/12/2005
|
|
|
||
|
La bisettrice di un angoloide (angolo solido) triedrico K, ha la proprietà di essere
il luogo geometrico dei punti equidistanti dalle facce di K.
Ovvero il luogo geometrico dei centri di infinite sfere che tangono le facce
di K. Tale bisettrice viene individuato
come retta comune ai piani bisettori i diedri di K (
vedi procedura in tav.7).
Esempio
Dati le proiezioni ortogonali di una piramide che ha per vertice il punto V e per base il triangolo ABC. Si vuole determinare la bisettrice dell'angoloide che ha vertice in V.
Procedura
- si determina il piano alpha come bisettore del diedro formato dalle facce VAB ed VAC ( clicca sulla fig.5 per ulteriori dettagli) - si determina il piano Beta come bisettore delle facce VBC ed VCA - si determina la bisettrice cercata b come retta d'intersezione tra i piani alpha e beta.
Verifica
si prende un punto O sulla bisettrice b, come centro di
una sfera che ha per raggio un segmento passante per Q e perpendicolare ad
una faccia del triedro K (Fig8/9). Si ha che tale sfera deve risultare
tangente alle altre due facce di K.
|
||
|
|
||
|
Angoloide Stabilito di avere tre o più piani aventi in comune un stesso punto V. In tal caso, si può notare che vi esistono quattro spazi che vengono detti angoloidi. In cui Ciascun è delimitati dalle facce di una piramide con vertice in V e di altezza indefinita. A secondo il numero di facce un angoloide viene detto triedro tetraedro pentaedro ... ecc. Le rette comuni alle facce di angoloide sono detti spigoli ed il punto in comune a tali spigoli viene detto vertice. Un angoloide viene, anche identificato con atri termini come: angolo solido o angolo poliedro. |
||
|
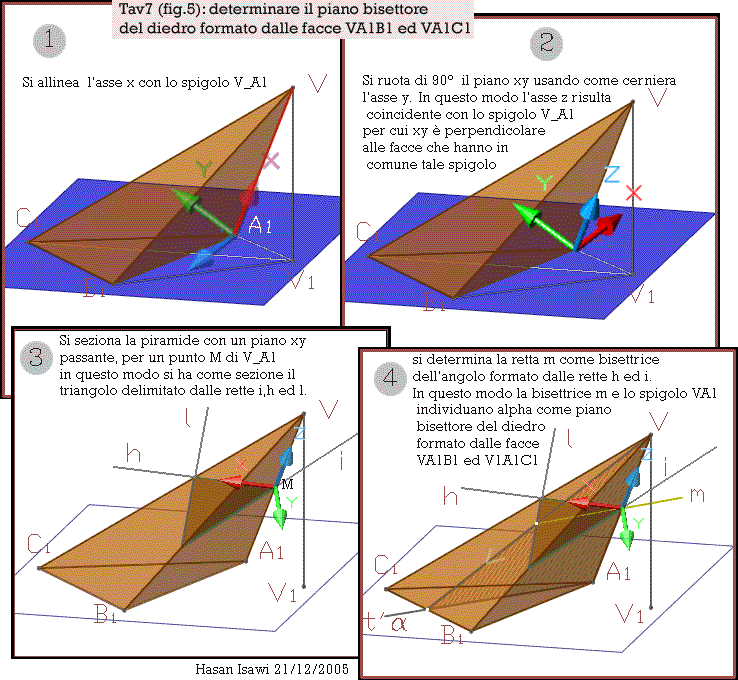
Tav.7 (Fig.5): determinare il
piano bisettore del diedro formato dalle facce che hanno in comune lo spigolo
V_A1
1- Si allinea l’asse x con lo spigolo V_A1 2- si ruota di 90° il piano xy usando come cerniera l’asse y. In questo modo l’asse z risulta coincidente con lo spigolo V_A1per cui xy è perpendicolare alle facce che hanno in comune tale spigolo 3- si seziona la piramide con un piano xy passante, per un punto M di V_A1in questo modo si ha come sezione il triangolo delimitato dalle rette i,h ed l. si determina la retta m come bisettrice dell’angolo formato dalle rette h ed i. In questo modo la bisettrice m e lo spigolo VA1 individuano alpha come piano bisettore del diedro formato dalle facce VA1B1 ed V1A1C1 |
||
|
||
Titolo: Determinazione della bisettrice di un angoloide
Procedura:
- Identificare i tre piani α, β e γ che formano l'angoloide.
- Determinare il piano bisettore δ di α e β:
- individuare la retta di intersezione r tra i piani α e β.
- Prendere un piano ortogonale alla retta r, che intersecherà α e β lungo due rette.
- Determinare la retta s che è la bisettrice dell'angolo formato dalle due rette d'intersezione del piano ortogonale e dei piani α e β.
- Determinare il piano bisettore φ di α e γ:Trova la retta di intersezione t tra i piani α e γ.
- Prendere un piano ortogonale alla retta t, che intersecherà α e γ lungo due rette.
- Determinare la retta u che è la bisettrice dell'angolo formato dalle due rette d'intersezione del piano ortogonale e dei piani α e γ.
- Determinare la retta di intersezione d tra i piani δ e φ.La retta d è la bisettrice dell'angoloide formato dai piani α, β e γ.
Nota: Per determinare il piano bisettore di un diedro formato da due piani α e β, segui i seguenti passaggi:
- Identificare i due piani α e β che formano il diedro.
- Trovare la retta di intersezione r tra i piani α e β.
- Costruire un piano ortogonale alla retta r, che intersecherà i piani α e β lungo due rette.
- La retta perpendicolare alla retta di intersezione r all'interno del piano ortogonale rappresenta la bisettrice del diedro formato dai piani α e β.
الاشتراك في:
الرسائل (Atom)




