بحث هذه المدونة الإلكترونية

24‏/09‏/2019

طرق الاظهار الهندسي- لمحة عامة

==============================================================
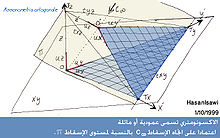
لقد كنت مدرسا لمادة الهندسة الوصفية لمدة 17 عاما في جامعة روما sapienza, ومنها 10 سنوات باستخدام ادوات الرسم التقليدية, وفي السنوات الاخيرة باستخدام ادوات الرسم الرقمية, في التخصص gestione del processo edilizio, وكان اسم المادة geometria descrittiva stages informatici, حيث كان هدف هذا الكورس التركيز على النمذجة ثلاثية الابعاد لاحجام معمارية مجردة, للوصول بعد ذلك الى إظهار هذه النماذج باستخدام جميع أساليب الإظهار من منظور واكسنومتري واسقاطات عمودية. وبالإضافة إلى ذلك الموضوعات المطلوبة كانت تشمل عمليات قياسية (خطية و زاويّة) وموضعية (تعامد, توازي, تماس,). من المسائل المهمة التي واجهناها تتعلق بالمحل الهندسي للنقاط المتساوية البعد بالنسبة لمستوين او ثلاثة مستويات أو أربعة مستويات. وفي هذه الحالة الأخيرة المحل الهندسي يتمثل في نقطة واحدة والتي يمكن ان تكون مركز كرة ماسة هذه المستويات الأربعة. والموضوع بشكل عام لا يتعلق بحل مسألة معينة بالذات, بل تمرين الذهن بواسطة مفاهيم الهندسة الوصفية على اكتشاف المجهول من مقاسات ومواضع.

طرق الاظهار الهندسي

تصنيف طرق الاظهار يعتمد اساسا على عملتين رئيسيتين وهما عملية الاسقاط وعملية التقاطع. عملية الاسقاط تكمن في تمرير خط مثلا r بنقطة معيينة في الفراغ مثلا A؛ اما عملية التقاطع فتكمن في تحديد نقطة التقاطع بين الخط r ومستوى باي. نقطة التقاطع بين الخط r والمستوى باي تسمى صورة النقطة A او إسقاط النقطة A ويرمز لها A'. المستوى باي يسمى مركز الإسقاط والذي يمكن ان يكون رأسي مائل او افقي.
تتنوع الإسقاطات إلى مركزية أو متوازية بالاعتماد على طبيعة مركز الإسقاط الذي يمكن ان يكون بالتوالي نقطة نهائية أو لانهائية.
  • نتائج
وكما قلنا سابقا مركز الاسقاط يمكن ان يكون نقطة لانهائية كما في حالة الاسقاط المركزي او نقطة لانهائية كما في الاسقاط المتوازي. هناك نوعين من الاسقاط المتوازي: الاسقاط العمودي (مثل الاكسنومتري العمودية وطريقة مونج) والاسقاط المائل مثل الاكسنومتري المائلة), وهذا يعتمد بالتوالي اذا كان اتجاه مركز الاسقاط عمودي او مائل بالنسبة لمستوى الاسقاط.

الاسقاط العمودي

نحصل على هذا النوع من الاسقاط عندما يكون اتجاه مركز الاسقاط عمودي على مستوى الاسقاط. تطبيقات هذا النوع من الاسقاط نجدها في طريقتين من الاظهار, وهما طريقة مونج, والاكسنومتري العمودية. الاكسنومتري تختلف عن طريقة مونج , بان هذه الاخيرة تعتمد مستويين اسقاط او اكثر, وبالتالي مركزين اسقاط او اكثر. أما في الاكسنومتري فهناك مركز اسقاط واحد ومستوى اسقاط واحد.

إسقاط متواز 


العناصر الأساسية في جميع انواع الاسقاط هي مركز ومستوى الاسقاط. وفقا لطبيعة مركز الاسقاط: نقطة نهائية او لانهائية, 
الاسقاط ينقسم إلى نوعين الإسقاط المتوازي والإسقاط المركزي (أو المنظور).

الظلال الناتجة من مصدر ضوء لانهائي تعتبر اسقاط متوازي. وفي الحالة التي تكون خطوط اشعة الضوء مائلة بالنسبة للمستوى المتلقي الظل, الاسقاطات تسمة اسقاطات مائلة

الظلال الناتجة من مركز ضوء نهائي, تعتبر اسقاط مركزي أو منظور

وبالتالي العناصر الأساسية في الإسقاطات المتوازية هي اتجاه الإسقاط D ومستوى الإسقاط p.[1][2][3] ووفقا للزاوية F المتشكلة بين D وp، الإسقاط المتوازي ينقسم إلى فئتين:
الإسقاط العمودي، عندما الزاوية F تكون قائمة بالنسبة للمستوى p.
الإسقاط المائل، عندما الزاوية F لا تساوي 90 درجة.

إسقاط مركزي

إلى التنقلاذهب إلى البحث


إسقاط مركزي
الإسقاط المركزي في الهندسة الوصفية هي عملية لتمثيل الاشكال الهندسية على سطح مستوي. من خلال عملية الإسقاط والتقاطع. العناصر الأساسية في الإسقاط المركزي هي:
  • نقطة نهائية تمثل مركز الإسقاط
  • وسطح مستوي يسمى مستوى الإسقاط.[1]
مثلاً, إذا اسقطنا خطين متوازيين (a, b) من نقطة نهائية (C)، فان صورتهما (a',b') سيلتقيان في نفس النقطة Ia التي تسمى نقطة التلاشي والتي تمثل صورة النقطة الانهائية أو صورة اتجاة تلك الخطوط (a, b).
من التطبيقات العملية للإسقاط المركزي هي المنظور.

طالع أيضا

الاسقاطات المتوازية

مصادر

  1. ^ Proiezione centrale نسخة محفوظة 05 مارس 2016 على موقع واي باك مشين.

إسقاط عمودي

هذا الإسقاط يشتمل على أساليب تمثيل هندسي مثل طريقة مونج والأكسونومتري العمودية: ايزوميترك (عندما تشكل المحاور xyz، زاوايا متساوية بالنسبة لمستوى الاسقاط)، ديمتريك (عندما اثنين من المحاور يشكلان زاوايتين متساويتين بالنسبة لمستوى الاسقاط. تريمترك ((عندما تشكل المحاور xyz، زاوايا مختلفة بالنسبة لمستوى الاسقاط)

إسقاط مائل




حسب التوازي أو عدمة بين أحد المستويات الاحداثية (xy, yz, xz) ومستوى الإسقاط π, يمكن تصنيف الإسقاط المائل إلى نوعين من الأكسونومتري: اكسونومتري كافاليرا، عندما يكون هناك توازي أو تطابق بين أحد المستويات الإحداثية ومستوى الاسقاط π . اكسونومتري عامة، عندما لا يوجد هناك توازي بين أحد المستويات الاحداثية مع π.


كافاليرا امامية

مراجع

  1. ^ Banerjee، Sudipto؛ Roy، Anindya (2014)، Linear Algebra and Matrix Analysis for Statistics، Texts in Statistical Science (الطبعة 1st)، Chapman and Hall/CRC، ISBN 978-1420095388
  2. ^ Doković، D. Ž. (August 1991). "Unitary similarity of projectors". Aequationes Mathematicae. 42 (1): 220–224. doi:10.1007/BF01818492.
  3. ^ قالب:Note autre projet

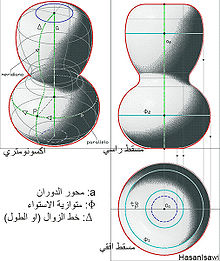
أكسونومتري


اذهب إلى التنقلاذهب إلى البحث

الاسقاط الموازي

اكسونومتري (الرسم على اليسار)
اكسونومتري- 'axonometric (من اليونانية áxon =محور وقياس = métron، ان يجري قياسها من خلال المحاور) هو إحدى طرق الاظهار الهندسي التي تعاملت معها الهندسة الوصفية. وقد اُدخل من قبل العالم الفرنسي غاسبار مونج في نهاية القرن الثامن عشر. المميزة الأساسية لطريقة الأكسونومتري هي القدرة على تمثيل، في نفس المستوى p، ثلاثة وجوه لحجم K ثلاثي الأبعاد ,هذا صحيح إذا اعتبرنا K متوازي متوازي السطوح أو ان K أي نوع من الحجوم ولكنه مغلف افتراضيا بمتوازي السطوح.
الأكسونومتري تسمى عمودية أو مائلة, اعتمادا على اتجاه الإسقاط بالنسبة لمستوى الإسقاط p.

تاريخ

أول مساهمات نظرية لدراسة الإظهار الاكسنومتري كانت لعالم الرياضيات الفرنسي جيرار ديساركوة (1593-1661) نحو 1630. ولكن هذه الدراسات لم تكن مفهومة كاملا من قبل معاصريه, وأعماله بقيت غير معروفة حتى أواخر القرن الثامن عشر تقريبا، عندما غاسبار مونج تعمق في هذه الدراسة. على الرغم من أن عمل مونج كان أساسي لجميع طرق التمثيل الهندسي، لكنة لم يتعمق في الإسقاط الاكسونومتري، بشكل نهائي. المساهمة الكبيرة اتت من الراهب الإنجليزي دبليو فاريش (W. Farish) فاريش (1759-1839)، بعد عامين من وفاة مونج، في 1820. وفي بيان تلي في كمبردج، وُضع الأساس النظري النهائي للاكسونومتري متساوية القياس (ايزومترك). تمثيل الاكسنومتري وجد تعريفا كاملا بعد بضع سنوات، عندما أساليب الإسقاط المتعامدة أصبحت أساليب علمية دقيقة في الوصف والتطبيق.
الجدارة العلمية لتدوين الاكسنومتري النهائي، يعود إلى العالم الألماني ول. ج. ويسباخ Weisbach ((1806 - 1871Ì، إضافة إلى أعمال بولك (Pohlke K. 1850) [1]

مصادر

  1. ^ دليل التصميم المعماري؛ الكاتب البروفوسور: [[[ماريو دوتشي]]؛ دار النشر: اتيرزا باري 2002- (Da M.Docci,
    Manuale di Disegno architettonico,
    Laterza Bari 2002)]

طالع أيضا

وصلات خارجية


إسقاطات عمودية (أو طريقة مونج)



اذهب إلى التنقلاذهب إلى البحث

إسقاطات متعامدة لتمثيل جسم ثلاثي الأبعاد، مرسومة في الفراغ (على يمين الصورة) وفي نفس المستوى (على اليسار)
طريقة مونج في الهندسة الوصفية هي طريقة تستعمل اسقاطات متوازية لتمثيل نماذج ثلاثية الأبعاد. وتستمد اسمها من عالم الرياضيات الفرنسي غاسبار مونج الذي يصفها في كتابه Géométrie descriptive 1799.طريقة مونج تعتمد على الإسقاطات المتعامدة للنموذج على مستويين متعامدين على بعضهما البعض، عادة ما يكون واحد منهما أفقي والآخر رأسي, وخط تقاطعهما يسمى خط الأرض.
بعد أن تتم عمليات الإسقاط نشرع في تدوير المستوى الرأسي حول خط ألأرض وبعكس عقارب الساعة, لجعله يتطابق مع المستوي الأفقي. هدف هذه العملية هو الحصول على مستوى واحد (أو بالاحرى مستويين متطابقين) لتسهيل قراءة وكتابة الرسم.
بالإضافة إلى ذلك من الممكن وضع الإسقاطات المتعامدة (مسقط افقي، وواجهة) لأي شكل هندسي في حالة تقابل, أي ان النقاط المتقابلة تنتمي إلى خطوط تلتقي في نقطة واحدة (نهائية أو لانهائية) تسمى مركز التقابل, والخطوط المتقابلة تلتقي في نقاط مصطفة على خط واحد يسمى محور التقابل.
من الجدير بالذكر أن الخطوط التي توصل النقاط المتقابلة تسمى خطوط تناظر. التي يكون اتجاهها عمودي على خط الأرض.

تمثيل الكيانات الهندسية الرئيسية

تمثيل نقطة


تمثيل النقطة في طريقة مونج
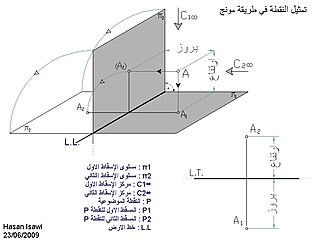
في طريقة مونج نقطة A في الفراغ تُمثل عن طريق إسقاطين عموديين على مستويات الإسقاط:π2 π1. نقطة التقاطع بين الخط العمودي المار بالنقطة A والمستوى الأفقي π1, هي المسقط الأول (أو الأفقي) للنقطة A ويُرمز لها A1. بطريقة مماثلة يحدد المسقط الثاني A2 كنقطة تقاطع بين π2 (مستوى الإسقاط الثاني) والخط العمودي على π2 والمار بالنقطة A.
  • المستوى الأفقي π1: يسمى مستوى الإسقاط الأول
  • المستوى الراسي π2: يسمى مستوى الإسقاط الثاني
  • ألاتجاه العمودي على π1 يسمى مركز الإسقاط الأول
  • ألاتجاه العمودي على π2 يسمى مركز الإسقاط الثاني
  • الخط العمودي على π1, يسمى خط الإسقاط الأول
  • الخط العمودي على π2, يسمى خط الإسقاط الثاني
  • ارتفاع A: مسافة (أو بُعد) النقطة A عن π1
  • بروز A: مسافة النقطة A عن π2

مثال

لنعين نقطة P في الزاوية الزوجية الأولى (I diedro), فعملية تحديد الإسقاطات المونجية للنقطة P تتم كما يلي:
  • الإسقاط الأول P1 للنقطة P, يحدد كنقطه تقاطع بين الخط الرأسي المار بالنقطة P والمستوى الأول π1 (يسمى أيضاً مستوى الإسقاط الافقي).
  • الإسقاط الثاني P2 للنقطة P, يحدد كنقطه تقاطع بين مستوى الإسقاط الثاني π2 (يسمى أيضاً مستوى الإسقاط الامامي) والخط العمودي على π2 (يسمى خط الإسقاطي الثاني).
المستوى المار بالنقطة P والعمودي على المستويين π1 وπ2, يقطعهما بخطين عموديين على خط الأرض. نقطة تقاطع هذا المستوى مع خط الأرض تسمى النقطة المرجعية ويرمز لها P0 (بي زيرو). وبهذا:
  • ارتفاع P = المسقيم P_P1 الذي يساوي أيضاً P2_P0
  • بروز P = المسقيم P_P2 الذي يساوي أيضاً P1_P0

تمثيل خط


تمثيل مونجي لخط عام
يتم تحديد الإسقاطات المتعامدة r1 r2 لخط r موضوع في الفراغ, كما يلي:
  • الإسقاط ألافقي r1 للخط r كتقاطع بين مستوى الإسقاط الأفقي π1 والمستوى الراسي المار بالخط r.
  • وبالمثل الإسقاط الراسي r2، يحدد كخط تقاطع بين مستوى الإسقاط الراسي π2 والمستوى العمودي على π2 والمار بالخط r.
عملياً، لتحديد الإسقاطات المونجية (r1 r2)، لخط r ,على سبيل المثال r1، من الضروري تحديد إسقاطين (P1 Q1) لنقطتين (P Q) ينتميان للخط r. ولأن الخط r نظريا يعتبر كيان غير محدودة، فالنقطتين يمكن أن يكونان آثار ذلك الخط r، أي نقاط التقاطع (T'r T"r) بين الخط r ومستويي الإسقاط (π2 π1).
    • نقطة التقاطع T'r بين خط r ومستوى الإسقاط الأفقي π1، تسمى الأثر الأول للخط r.
    • أما نقطة التقاطع T"r بين خط r ومستوى الإسقاط الرأسي π2، تسمى الأثر الثاني للخط r.

تمثيل مستوى


مستويي الاسقاط في طريقة مونج
المستوى من الناحية النظرية يعتبر لانهائي, وبالتالي الطريقة الوحيدة لتمثيله يتم من خلال خطوط تقاطعه مع مستويات الاسقاط. وهذه الخطوط تسمى اثار المستوى. مثلا تقاطع مستوى الفا مع مستوى الاسقاط الأول يسمى الاثر الأول للمستوى الفا, وخط تقاطع الفا مع مستوى الاسقاط الثاني يسمى الاثر الثاني للمستوى الفا.

تاريخ

مونج تعهد بعدم الكشف عن الطريقة الموصوفة أعلاه، التي كانت سر عسكري لمده 15 عاما. فقط في 1794، سمح بتدريسها في باريس. [1]

ببليوغرافيا

مصادر

  1. ^ Gaspard Monge: Founder of descriptive geometry نسخة محفوظة 29 أبريل 2013 على موقع واي باك مشين.

وصلات خارجية

Posted by at

ليست هناك تعليقات:

إرسال تعليق

الاشتراك في: تعليقات الرسالة (Atom)