=====================================================================
يهدف هذا البحث إلى دراسة المحل الهندسي لمراكز الكرات المتماسة لثلاث أسطح رباعية معلومة (الإهليلج، الزائد، المكافئ، الأسطوانة، المخروط). وسيتم التركيز بشكل خاص على تحديد الشروط الكافية والضرورية لوجود مثل هذه الكرات. ومن ثم، استغلال هذه النتائج لنمذجة أسطح عضوية معقدة، وذلك من خلال تحديد السطح المغلف لهذه الكرات.
سيتم استخدام أدوات الهندسة الوصفية والإسقاطية، بالإضافة إلى برمجيات الحاسوب المتخصصة، لتحقيق الأهداف المذكورة.
الهدف النهائي من هذا البحث المساهمة في تطوير أدوات
هندسية بديلة لتصميم الأسطح العضوية المعقدة، وتوفير أساس نظري قوي لتعليم طلاب العمارة والتصميم.
la ricerca riguarda la stesura di procedimenti geometrici descrittivi 3d atti alla determinazione dei luoghi geometrici dei punti equidistanti da due o piu superfici di rotazione
This research concerns the drawing up of 3d descriptive geometric procedures aimed to determine the geometric loci of the points equidistant from two or more quadrics
la ricerca riguarda la stesura di procedimenti geometrici descrittivi 3d atti alla determinazione dei luoghi geometrici dei punti equidistanti da due o piu superfici di rotazione
le bisettroide di due superficie di rotazione: cono e clindro
(السطح المنصف لسطحين دائريين: مخروط و اسطوانة)
le generatrici della bisettroide in questione si ottengono nella maggior parte dei casi come luogo geometrico dei punti equidistanti da due coniche, eventualmente degeneri. il modo più semplice per ottenere tali coniche consiste nel utilizzare dei piani secanti passanti per il vertice del cono. ciascun dei quali seziona il cono secondo due generatrici, e seziona il cilindro nella maggior parte dei casi secondo un ellisse. il luogo geometrico dei punti equidistanti dalle generatrici del cono e dalle ellissi del cilindro sono le generatrici della bisettroide. Tale luogo geometrico nella maggior parte delle citate coniche e' una parabola.
 |
bisettroide di due superficie di rotazione: cono e clindro
السطح المنصف لسطحين دائريين: مخروط و اسطوانة
|
come abbiamo detto : il luogo geometrico dei punti equidistanti dalle due date superfici di rotazioni rappresenta le generatrici della bisettroide cercata. ma poiché esistono due e non una parabole come luoghi geometrici dei punti equidistanti da un retta (sezione del cono) e da un ellisse (sezione del cilindro), allora sono due le bisettroidi cercate
 |
| esistono due bisettroidi tra le due superfici di rotazione date : cono e cilindro |
 |
la giustificazione spaziale della parabola come luogo geometrico dei punti equidistanti da una retta e una circonferenza
|
prima di verificare che la bisettroide ottenuta come luogo geometrico dei centri delle sfere tangenti due superfici di rotazione (in questo caso cono e cilindro) sia paraboloide iperbolico (seguendo il suggerimento del prof.
Reccardo migliari), . devo necessariamente ricordare che sezionando il paraboloide iperbolico con dei piani perpendicolare al suo asse si ottengono delle parabole, e con dei piani paralleli all'asse si ottengono delle iperboli. inoltre il paraboloide iperbolico è anche una superficie doppiamente rigata. per cui per ogni suo punto passano due rette appartenenti per intero alla stessa superficie. quindi possiamo dire che se si va ad eseguire delle sezioni piane sulla detta bisettroide, e non si ottiene come risultato delle sezioni delle rette, parabole o iperbole, significa che la bisettroide non e' un paraboloide iperbolico ?
 |
| sezioni parabolici ed iperbolici della bisettroide |
 |
nel disegno di sinistra sono dati rispettivamente la prima proiezione di un cono di rotazione K ,
e la seconda proiezione di K e di una sfera tangente K.
Si vuole determinare la prima proiezione di una delle due sfere tangente K |
 |
determinare una sfera di raggio assegnato in modo che sia tangente un cilindro ed un cono in una generatrice data del cilindro
|
 |
تحديد الكرة بنصف قطر معلوم بحيث تكون متماسة لسطحين دائريين: مخروط واسطوانة. وبشرط مرور الكرة برأس المخروط
Determinare la sfera di raggio assegnato tangente un cilindro ed un cono. Nella condizione che passi la sfera per il vertice del cono. |
Se il luogo geometrico di tutte le sfere tangenti due superfici di rotazioni intersecanti, e' simile alla loro curva d'intersezione, allora come sara il luogo geometrico in assenza d'intersezione ?
 |
Il luogo geometrico dei centri delle sfere tangenti due superfici di rotazioni non intersecanti tra loro
المحل الهندسي لمراكز الكرات المتماسة سحطين دائريين غير متقاطعين فيما بينهما |
In questo modo sarebbe interessante poter modellare la superficie di un progetto architettonico come luogo geometrico di due o più superfici di rotazione, eventualmente degeneri in superficie piana ...
Nel caso in cui le due superficie non sono intersecanti tra loro, si ha che ciascuna generatrice della bisettrice cercata e' una quartica monogrammica simile alla quartica che si ottiene quando si costruiscono le superfici parallele alle due superficie di rotazione date, di una medesima distanza. inoltre si fa notare che la citata quartica si degenera in un punto quando le dette due superfici parallele sono tangenti tra loro.
la domanda iniziale
determinare una sfera tangente due superfici di rotazione: cono e clindro, nella condizione che passi per un punto P dato appartenente ad una generatrice g del cilindro ( o ad una generatrice del cono)
Risposta
il luogo geometrico dei centri delle sfere che soddisfano tale condizione puo essere una parabola .
quindi esistono infinite sfere che passano per P.
la soluzione consiste nel determinare la bisettrice delle due superfici , ovvero la superficie che funge da luogo geometrico dei centri delle sfere tangenti tali superfici, e poi di condurre per P la retta r perpendicolare alla superficie del cilindro. dove la retta r incontra la superficie della bisettroide, si ha il centro della sfera passante per P e tangente le superficie date.
 |
| verificando la curva ottenuta (colore blu) che funge da luogo geometrico dei centri delle sfere tangenti tre coni non corrispondenti si ha' una curva sghemba e non piana |
 |
| la determinazione delle due superfici di raccordo tangenziale (diretto ed inverso) tra tre cono di rotazione non corrispondenti tra loro |
 |
| Sono visualizzati di più le linee di costruzione del risultato sopra |
 |
Raccordo tangenziale tra tre cilindri di rotazione non intersecanti tra loro.
anche in panorama
|
 |
| in trasparenza |
 |
analogamente alle superfici rigate, per determinare una superficie di raccordo tangenziali vi servono tre direttrici, che in questo caso sono un punto, una retta ed un piano
|
https://isawi.blogspot.com/2019/04/luoghi-geometrici.html
 |
| analogamente ad un triangolo, dove esiste l'incentro e il circocentro, anche per un piramide triangolare R, esiste nello spazio l'ncentroide e il circocentroide di una piramide triangolare R, che sono rispettivamente i centri di due sfere, una tangente gli spigoli di R e l'altra tangente le facce di R. e poiché la piramide triangolare e' composta da 4 angoloidi triedrici, per cui e' sufficiente determinare, come e' stato parzialmente illustrato nel caso allegato, i luoghi dei centri delle sfere inscriventi e quelli circoscriventi ciascun di tali angoloidi. e poi si va a determinare rispettivamente i loro punti d'intersezione per avere i cosiddetti incentroide e circocentroide di una piramide triangolare |
 |
Geometric Loci | Hasan Isawi | 14 updates | Research Project.
Dati 4 punti non appartenenti ad un stesso piano si ha una piramide triangolare K. l'incentroide di K si determina come punto comune alle bisettrici dei 4 angoloidi formanti K. e quindi tale punto rappresenta il centro della sfera tangenti tutte facce di K
|
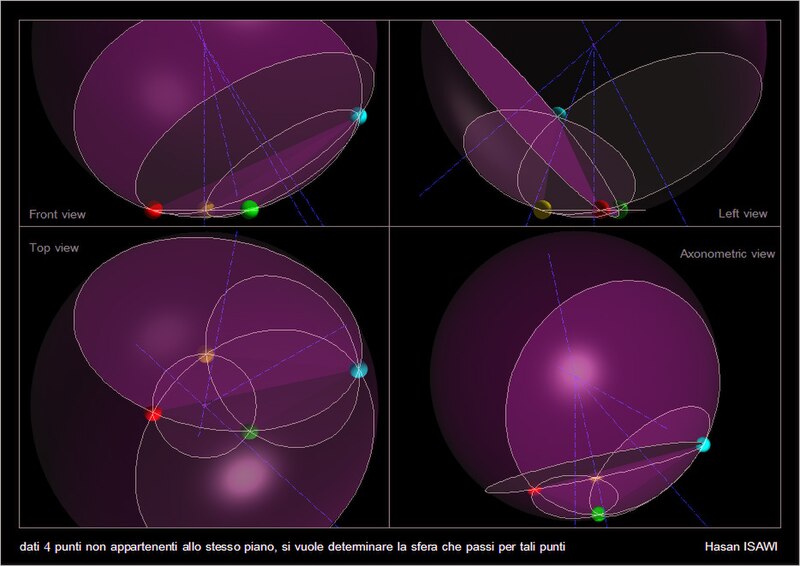 |
Determine circumscribed sphere of an arbitrary tetrahedron, or in other words determine the sphere passing through 4 points not belonging to the same plane
la sfera individuata da 4 punti non appartenenti allo stesso piano
Analogamente al fatto che tre punti non allineati individuano una circonferenza, si può dire la stessa cosa nello spazio quando sono dati 4 punti non appartenenti allo stesso piano individuano una sfera.
poiché 4 punti non appartenenti allo stesso piano individuano un tetraedro, allora il centro di tale sfera rappresenta l'incentroide del tetraedro
https://www.researchgate.net/project/Geometric-Loci
|
 |
| luogo geometrico dei punti di tangenza di superfici superfici con due date superfici di rotazione generiche tra loro |
 |
| luogo geometrico dei centri due sfere tangenti a due sfere interne tra loro |
 |
| out of equator: determinata la quinta sfera tangente a 4 sfere tangenti tra loro |
 |
| solo sul bordo altrimenti tre a tre |
 |
| iperbole come conica di tangenza inversa tra due coniche generiche |
 |
la ricerca si sta volgendo ad un bel termine ☺️
intanto si può dire che lavorando nel piano forse si può risolvere un solo problema ed un solo caso, e poi ripetere la soluzione in modo meccanico, ma solo ritornando allo spazio alle origine delle figure che hanno prodotto tali proiezioni, che si può generalizzare il problema e risolvere la maggior parte dei casi . quindi si può dire che la giustificazione spaziale delle cose e' come uscire dalla caverna platonica
الانشاءات الهندسية بين الاسقاطات قد تحل مسألة معينة وفي حالة واحدة فقط، وبعد ذلك يمكن تكرار الحل ميكانيكيا. ولكن من خلال العودة إلى أصل الاشكال التي أنتجت تلك الاسقاطات، من الممكن تعميم المسألة وتبرير مجموعة كبيرة من الحالات. ولذلك يمكن تشبيه التبرير الفراغي بعملية الخروج من الكهف الأفلاطوني😉 |
 |
Invece di avere i soliti applicativi con limitati operazioni di montaggio e smontaggio,
ce un spazio geometrico infinito tutto .da scoprire.
Tre fasci proiettivi che hanno in comune una stessa conica
|
interruzione primo semestre 2019
 |
| il luogho dei centri delle sfere tangenti due rette ed una sfera |
 |
| | | Superficie di raccordo tangenziale tra una sfera e due cilindri circolari |
-----------------------------------End



































